题目内容
18.若过点(2,0)的直线与曲线y=x3和y=ax2+7x-4都相切,则a=2或$-\frac{49}{16}$.分析 设过曲线y=x3上的点P(t,t3)的切线过点(2,0),对函数y=x3求导,求得切线的斜率和切线的方程,将(2,0)代入方程,解得t=0和3,分别讨论t,求出y=ax2+7x-4的导数,可得切线的斜率,求得切点的坐标,代入切线的方程,可得a的值.
解答 解:设过曲线y=x3上的点P(t,t3)的切线过点(2,0),
对函数y=x3求导得y'=3x2,
故曲线y=x3上的点P(t,t3)的切线方程为y-t3=3t2(x-t),即y=3t2x-2t3,
将点(2,0)的坐标代入此切线方程得0=3t2×2-2t3,即2t2(3-t)=0,
解得t=0或t=3,
(1)当t=0时,则切线方程为y=0,即切线为x轴,此时曲线y=ax2+7x-4与x轴相切,
则$△={7^2}-4×a×({-4})=49+16a=0⇒a=-\frac{49}{16}$;
(2)当t=3时,切线的方程为y=27x-54,
对函数y=ax2+7x-4求导得y'=2ax+7,
令y'=27,则有2ax+7=27,解得$x=\frac{10}{a}$,
将$x=\frac{10}{a}$代入y=ax2+7x-4得$y=a•{({\frac{10}{a}})^2}+7×\frac{10}{a}-4=\frac{170}{a}-4$,
即切点坐标为$({\frac{10}{a},\frac{170}{a}-4})$代入切线方程得$\frac{170}{a}-4=27×\frac{10}{a}-54$,
化简得$\frac{100}{a}=50$,解得a=2,
综上所述a=2或$a=-\frac{49}{16}$.
故答案为:a=2或$a=-\frac{49}{16}$.
点评 本题考查导数的运用:求切线的斜率,考查导数的几何意义:函数在某点处的导数即为曲线在该点处的切线的方程,考查直线方程的运用,属于中档题.

| A. | (-∞,1) | B. | (1,+∞) | C. | (-∞,1] | D. | [1,+∞) |
①若m⊥α,m⊥β,则α∥β;②若α⊥γ,β⊥γ,则α∥β
③若m∥α,m∥β,则α∥β;④l∥α,m?α,则l∥m.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | (-∞,-2]∪{1} | B. | (-∞,-2]∪[1,2] | C. | [1,+∞) | D. | [-2,1] |
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | 1-i | B. | -1+i | C. | 1+i | D. | -1-i |
 如图,梯形ABCD中,AB∥CD,BC=6,tan∠ABC=-2$\sqrt{2}$.
如图,梯形ABCD中,AB∥CD,BC=6,tan∠ABC=-2$\sqrt{2}$.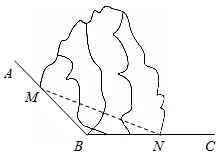 如图所示,AB,BC是两条傍山公路,∠ABC=120°,现在拟从M,N两处修建一条隧道(单位:千米).
如图所示,AB,BC是两条傍山公路,∠ABC=120°,现在拟从M,N两处修建一条隧道(单位:千米).