题目内容
某中学一名数学老师对全班50名学生某次考试成绩分男女生进行了统计(满分150分),其中120分(含120分)以上为优秀,绘制了如下的两个频率分布直方图:

男生
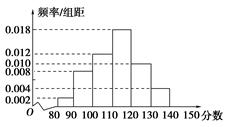
女生
(1)根据以上两个直方图完成下面的2×2列联表:
(2)根据(1)中表格的数据计算,你有多大把握认为学生的数学成绩与性别之间有关系?
(注:
K2=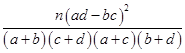 ,其中n=a+b+c+d.)
,其中n=a+b+c+d.)
(3)若从成绩在[130,140]的学生中任取2人,求取到的2人中至少有1名女生的概率.

男生

女生
(1)根据以上两个直方图完成下面的2×2列联表:
| 成绩性别 | 优秀 | 不优秀 | 总计 |
| 男生 | | | |
| 女生 | | | |
| 总计 | | | |
(2)根据(1)中表格的数据计算,你有多大把握认为学生的数学成绩与性别之间有关系?
(注:
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K2=
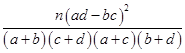 ,其中n=a+b+c+d.)
,其中n=a+b+c+d.)(3)若从成绩在[130,140]的学生中任取2人,求取到的2人中至少有1名女生的概率.
(1)
(2)有95%的把握认为学生的数学成绩与性别之间有关系
(3)
| 成绩性别 | 优秀 | 不优秀 | 总计 |
| 男生 | 13 | 10 | 23 |
| 女生 | 7 | 20 | 27 |
| 总计 | 20 | 30 | 50 |
(2)有95%的把握认为学生的数学成绩与性别之间有关系
(3)

(1)
(2)由(1)中表格的数据知, K2= ≈4.844.
≈4.844.
∵K2≈4.844≥3.841,∴有95%的把握认为学生的数学成绩与性别之间有关系.
(3)由题知,成绩在[130,140]范围内的男生有4人、女生有2人,分别记为A1,A2,A3,A4,B1,B2,从中任取2人共有(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,A4),(A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2)15种不同结果,且事件“其中至少有1名女生”包含了9种不同结果.
∴所求事件的概率P= =
= .
.
| 成绩性别 | 优秀 | 不优秀 | 总计 |
| 男生 | 13 | 10 | 23 |
| 女生 | 7 | 20 | 27 |
| 总计 | 20 | 30 | 50 |
(2)由(1)中表格的数据知, K2=
 ≈4.844.
≈4.844.∵K2≈4.844≥3.841,∴有95%的把握认为学生的数学成绩与性别之间有关系.
(3)由题知,成绩在[130,140]范围内的男生有4人、女生有2人,分别记为A1,A2,A3,A4,B1,B2,从中任取2人共有(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,A4),(A3,B1),(A3,B2),(A4,B1),(A4,B2),(B1,B2)15种不同结果,且事件“其中至少有1名女生”包含了9种不同结果.
∴所求事件的概率P=
 =
= .
.
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 136,z
136,z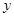 =
=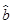 x+
x+
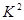
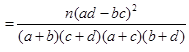 (
( )
)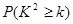
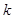
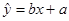 必过点
必过点  份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在
份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在 的学生人数为6.
的学生人数为6. 和
和 这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在
这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在


 对
对 的线性回归方程为( )
的线性回归方程为( ) B.
B.  C.
C.  D.
D. 