题目内容
4. 如图,直三棱柱ABC-A1B1C1中,D是AB的中点.
如图,直三棱柱ABC-A1B1C1中,D是AB的中点.(1)证明:BC1∥平面A1CD;
(2)设AA1=AC=CB=2,AB=2$\sqrt{2}$,求异面直线BC1与A1D所成角的大小.
分析 (1)根据线面平行的判定定理即可证明BC1∥平面A1CD;
(2)根据异面直线所成角的定义进行求解即可.
解答 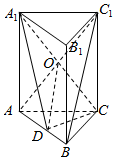 (1)证明:连结AC1,交A1C于点O,连结OD,
(1)证明:连结AC1,交A1C于点O,连结OD,
因为D是AB的中点,所以BC1∥OD,
因为BC1?平面A1CD,OD?平面A1CD,
所以BC1∥平面A1CD.
(2)解:结合(1)易知∠A1DO即为异面直线A与D,E所成角,
因为AC=BC,D为AB的中点,所以CD⊥AB,
又因为该三棱柱是直三棱柱,所以CD⊥平面ABB1A1,
即CD⊥平面A1DE,∵$A{A_1}=AC=CB=2,AB=2\sqrt{2}$,
∴${A_1}D=\sqrt{6},DO={A_1}O=\frac{1}{2}{A_1}C=\sqrt{2}$,
∴$cos∠{A_1}DO=\frac{{\sqrt{3}}}{2}$,∴$∠{A_1}DO=\frac{π}{6}$.
点评 本题主要考查线面平行的判定以及异面直线所成角的求解,利用相应的判定定理以及异面直线所成角的定义是解决本题的关键.

练习册系列答案
相关题目
 某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图:
某篮球队对篮球运动员的篮球技能进行统计研究,针对篮球运动员在投篮命中时,运动员在篮筐中心的水平距离这项指标,对某运动员进行了若干场次的统计,依据统计结果绘制如下频率分布直方图: