题目内容
3.对某两名高三学生在连续9次数学测试中的成绩(单位:分)进行统计得到如下折线图.下面关于这两位同学的数学成绩的分析中,正确的共有( )个.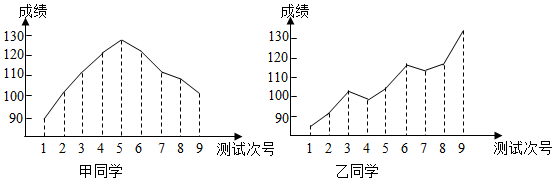
①甲同学的成绩折线图具有较好的对称性,与正态曲线相近,故而平均成绩为130分;
②根据甲同学成绩折线图提供的数据进行统计,估计该同学平均成绩在区间[110,120]内;
③乙同学的数学成绩与考试次号具有比较明显的线性相关性,且为正相关;
④乙同学在这连续九次测验中的最高分与最低分的差超过40分.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据折线图分别判断①②③④的正误即可.
解答 解:①甲同学的成绩折线图具有较好的对称性,最高分是130分,故而平均成绩小于130分,①错误;
②根据甲同学成绩折线图提供的数据进行统计,估计该同学平均成绩在区间[110,120]内,②正确;
③乙同学的数学成绩与考试次号具有比较明显的线性相关性,且为正相关,③正确;
④乙同学在这连续九次测验中的最高分大于130分,最低分小于90分,差超过40分,故④正确;
故选:C.
点评 本题考查了频率分布折线图,考查数形结合,是一道基础题.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
11.已知实数1,t,4成等比数列,则圆锥曲线$\frac{x^2}{t}+{y^2}$=1的离心率为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$或$\sqrt{3}$ | C. | $\frac{1}{2}$或$\sqrt{3}$ | D. | $\frac{{\sqrt{2}}}{2}$或3 |
15.观察如图:

则第( )行的各数之和等于20112.

则第( )行的各数之和等于20112.
| A. | 2010 | B. | 2009 | C. | 1006 | D. | 1005 |
12.如图,根据样本的频率分布直方图,估计样本的中位数是( )


| A. | 10 | B. | 12 | C. | 13 | D. | 16 |
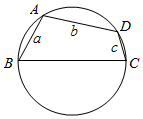 如图,设圆内接四边形ABCD的边BC为圆的直径,其余三边为a、b、c,求证:这个圆的直径是方程x3-(a2+b2+c2)x-2abc=0的根.
如图,设圆内接四边形ABCD的边BC为圆的直径,其余三边为a、b、c,求证:这个圆的直径是方程x3-(a2+b2+c2)x-2abc=0的根.