题目内容
已知a与b均为单位向量,其夹角为θ,有下列四个命题
p1:|a+b|>1⇔θ∈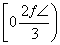
p2:|a+b|>1⇔θ∈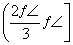
p3:|a-b|>1⇔θ∈
p4:|a-b|>1⇔θ∈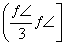
其中真命题的个数是____________.
2
解析 由|a+b|>1可得a2+2a·b+b2>1,因为|a|=1,|b|=1,所以a·b>- ,故θ∈
,故θ∈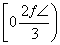 .当θ∈
.当θ∈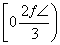 时,a·b>-
时,a·b>- ,|a+b|2=a2+2a·b+b2>1,即|a+b|>1,故p1正确.由|a-b|>1可得a2-2a·b+b2>1,因为|a|=1,|b|=1,所以a·b<
,|a+b|2=a2+2a·b+b2>1,即|a+b|>1,故p1正确.由|a-b|>1可得a2-2a·b+b2>1,因为|a|=1,|b|=1,所以a·b< ,故θ∈
,故θ∈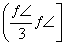 ,反之也成立,p4正确.
,反之也成立,p4正确.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,又知BA1⊥AC1.
(1)求证:AC1⊥平面A1BC;
(2)求二面角A-A1B-C的余弦值.

已知函数f(x)、g(x)分别由下表给出:
| x | 1 | 2 | 3 |
| f(x) | 1 | 3 | 1 |
| x | 1 | 2 | 3 |
| g(x) | 3 | 2 | 1 |
则f[g(1)]的值为________;满足f[g(x)]>g[f(x)]的x的值是________.
 -a-b,那么φ(a,b)=0是a与b互补的( ).
-a-b,那么φ(a,b)=0是a与b互补的( ). 则f(f(5))=( ).
则f(f(5))=( ).