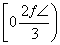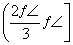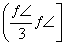题目内容
三棱柱ABC-A1B1C1,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,又知BA1⊥AC1.
(1)求证:AC1⊥平面A1BC;
(2)求二面角A-A1B-C的余弦值.

解:(1)证明:如图,设A1D=t(>0),取AB的中点E,则DE∥BC,
因为BC⊥AC,所以DE⊥AC,又A1D⊥平面ABC,
所以DE,DC,DA1为x,y,z轴建立空间直角坐标系,

则A(0,-1,0),C(0,1,0),B(2,1,0),A1(0,0,t),C1(0,2,t),
 =(0,3,t),
=(0,3,t), =(-2,-1,t),
=(-2,-1,t),
 =(2,0,0), 由
=(2,0,0), 由 ·
· =0,知AC1⊥CB,
=0,知AC1⊥CB,
又BA1⊥AC1,BA1∩CB=B,从而AC1⊥平面A1BC;
.
(2)由 ·
· =-3+t2=0,得t=
=-3+t2=0,得t=
设平面A1AB的法向量为n=(x,y,z),
 =(0,1,
=(0,1, ),
),  =(2,2,0),
=(2,2,0),
所以 ,设z=1,则n=(
,设z=1,则n=( ,-
,- ,1). .
,1). .
再设平面A1BC的法向量为m=(u,v,w), =(0,-1,
=(0,-1, ),
),  =(2,0,0),
=(2,0,0),
所以 , 设w=1,则m=(0,
, 设w=1,则m=(0, ,1),
,1),
故cos〈m,n〉= =-
=- ,
,
因为二面角A-A1B-C为锐角,所以可知二面角A-A1B-C的余弦值为 .
.

练习册系列答案
相关题目
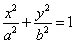
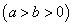 的离心率为
的离心率为 ,其左、右焦点分别为F1,F2,点P是坐标平面内一点,且|OP|=
,其左、右焦点分别为F1,F2,点P是坐标平面内一点,且|OP|=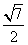 ,
,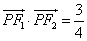 (O为坐标原点)。
(O为坐标原点)。  的直线L与该椭圆相交于M、N两点,且
的直线L与该椭圆相交于M、N两点,且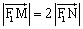 ,求直线L的方程。
,求直线L的方程。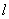
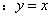 与圆
与圆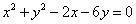 相交于
相交于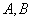 两点,则
两点,则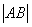 =________.
=________. ,
, 〉的值为( )
〉的值为( ) B.
B. C.
C. D.
D.

 }的前n 项和为
}的前n 项和为 ,已知
,已知 ,
, ,
, 成等差数列
成等差数列 ; (2)求
; (2)求 -
- =3,求
=3,求 的前
的前 项和为
项和为 ,若
,若 ,则数列
,则数列 B.1 C.2 D.3
B.1 C.2 D.3 、
、 、
、 成等比数列,且
成等比数列,且 ,若
,若 ,
, 为正常数,则
为正常数,则 B.
B. C.
C. D.
D.
 则
则 是
是 的 ( )
的 ( )