题目内容
若O为平面内任一点，且满足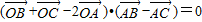
，则△ABC一定是（ ）A．等腰三角形
B．直角三角形
C．等腰直角三角形
D．等边三角形
【答案】分析：把已知等式中的2
拆为两项，利用向量的三角形法则变形后，再根据平方差公式化简，得到
与
的模相等，即可判断出此三角形为等腰三角形．
解答：解：∵
=[（
-
）+（
-
）]•（
-
）
=（
+
）•（
-
）
=|
|2-|
|2=0，即|
|=|
|，
∴△ABC一定是等腰三角形．
故选A
点评：此题考查了三角形的形状判定，平面向量的计算法则，以及平方差公式，把已知等式中的
变为（
-
）+（
-
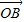）是本题的突破点．
拆为两项，利用向量的三角形法则变形后，再根据平方差公式化简，得到与的模相等，即可判断出此三角形为等腰三角形．解答：解：∵
=[（
-）+（-）]•（-）=（
+）•（-）=|
|2-||2=0，即||=||，∴△ABC一定是等腰三角形．
故选A
点评：此题考查了三角形的形状判定，平面向量的计算法则，以及平方差公式，把已知等式中的
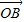变为（-）+（-）是本题的突破点． 
练习册系列答案
阅读快车系列答案
相关题目
若O为平面内任一点，且满足(
+
-2
)•(
-
)=0，则△ABC一定是（ ）
| OB |
| OC |
| OA |
| AB |
| AC |
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
+
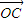-2
）•（
-
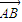）=0，则△ABC是（ ）