题目内容
若O为平面内任一点且(
+
-2
)•(
-
)=0,则△ABC是( )
| OB |
| OC |
| OA |
| AB |
| AC |
分析:利用向量的运算可得到|
|=|
|,即AB=AC,从而可判断出答案.
| AB |
| AC |
解答:解:(
+
-2
)(
-
)=0得(
+
)(
-
)=0,
∴
2-
2=0,即|
|=|
|,
∴AB=AC.
∴△ABC是等腰三角形,但不一定是直角三角形.
故选C.
| OB |
| OC |
| OA |
| AB |
| AC |
| AB |
| AC |
| AB |
| AC |
∴
| AB |
| AC |
| AB |
| AC |
∴AB=AC.
∴△ABC是等腰三角形,但不一定是直角三角形.
故选C.
点评:本题考查向量的运算,通过向量的运算考查三角形的形状判断,属于中档题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 +
+ -2
-2 )•(
)•( -
- )=0,则△ABC是( )
)=0,则△ABC是( ) +
+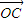 -2
-2 )•(
)•(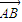 -
- )=0,则△ABC是( )
)=0,则△ABC是( )