题目内容
已知圆C的圆心在坐标原点，且过点M（1，
）．
（1）求圆C的方程；
（2）若直线l与圆C相切于点M，求直线l的方程．
| 3 |
（1）求圆C的方程；
（2）若直线l与圆C相切于点M，求直线l的方程．
考点：直线与圆的位置关系,圆的切线方程,直线和圆的方程的应用
专题：直线与圆
分析：（1）根据条件求圆的半径即可求圆C的方程；
（2）根据直线和圆相切的等价条件，求直线l的方程．
（2）根据直线和圆相切的等价条件，求直线l的方程．
解答：
解：（1）由题意可得圆C的半径r=|OM|=
=2，
再根据原点为圆心，
可得圆的方程为 x2+y2=4．
（2）若直线l与圆C相切于点M（1，
），
故直线l的斜率为
=
=-
，
由点斜式求得直线l的方程为 y-
=-
（x-1），
即x+
y-4=0．
12+(
|
再根据原点为圆心，
可得圆的方程为 x2+y2=4．
（2）若直线l与圆C相切于点M（1，
| 3 |
故直线l的斜率为
| -1 |
| kOM |
| -1 | ||||
|
| ||
| 3 |
由点斜式求得直线l的方程为 y-
| 3 |
| ||
| 3 |
即x+
| 3 |
点评：本题主要考查圆的标准方程的求解，以及直线和圆相切的应用，利用直线和圆的位置关系是解决本题的关键．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
下列直线中与x-y+1=0平行的是（ ）
| A、x+y=-1 |
| B、x+y=1 |
| C、2x-2y=-2 |
| D、2x-2y=2 |
等比数列{an}的前n项的和为Sn，若4a1，2a2，a3成等差数列，则
的值是（ ）
| S4 |
| a4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
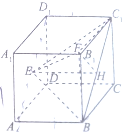已知正方体ABCD-A1B1C1D1棱长为1，E、F、H分别为面A1ADD1、面DCC1D1与面BCC1B1的中心．