题目内容
如图,抛物线 的顶点为坐标原点
的顶点为坐标原点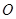 ,焦点
,焦点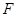 在
在 轴上,准线
轴上,准线 与圆
与圆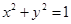 相切.
相切.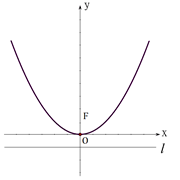
(Ⅰ)求抛物线 的方程;
的方程;
(Ⅱ)已知直线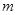 和抛物线
和抛物线 交于点
交于点 ,命题P:“若直线
,命题P:“若直线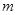 过定点
过定点 ,则
,则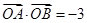 ”,请判断命题P的真假,并证明。
”,请判断命题P的真假,并证明。
(Ⅰ)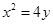 (Ⅱ)命题P为真命题
(Ⅱ)命题P为真命题
解析试题分析:(Ⅰ)依题意,可设抛物线 的方程为
的方程为 ,
,
其准线 的方程为
的方程为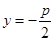 .
.
∵准线 与圆
与圆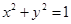 相切,
相切,
∴所以圆心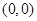 到直线
到直线 的距离
的距离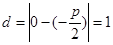 ,解得
,解得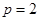 .
.
故抛物线 的方程为:
的方程为: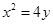 .
.
(Ⅱ)命题P为真命题
因为直线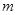 和抛物线
和抛物线 交于点
交于点 且过定点
且过定点 ,所以直线
,所以直线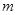 的斜率
的斜率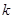 一定存在
一定存在
设直线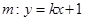 ,交点
,交点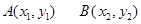 联立抛物线
联立抛物线 的方程
的方程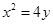 ,
,
得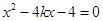
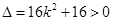 恒成立
恒成立
由韦达定理得
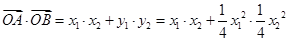
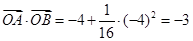 ,所以命题P为真命题
,所以命题P为真命题
考点:直线与圆锥曲线的综合问题;恒过定点的直线;抛物线的标准方程.
点评:本题考查了抛物线方程的求法,以及直线与抛物线的位置关系判断,做题时要认真分析,避免不必要的错误.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
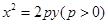 ,直线
,直线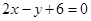 截抛物线C所得弦长为
截抛物线C所得弦长为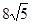 .
.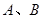 是抛物线上异于原点
是抛物线上异于原点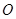 的两个动点,记
的两个动点,记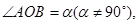 若
若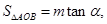 试求当
试求当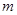 取得最小值时
取得最小值时 的最大值.
的最大值.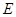 :
: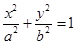 (
(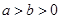 )过点
)过点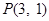 ,其左、右焦点分别为
,其左、右焦点分别为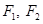 ,且
,且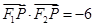 .
.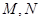 是直线
是直线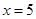 上的两个动点,且
上的两个动点,且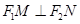 ,则以
,则以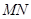 为直径的圆
为直径的圆 是否过定点?请说明理由.
是否过定点?请说明理由.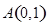 、
、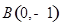 ,
, 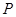 是一个动点, 且直线
是一个动点, 且直线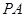 、
、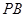 的斜率之积为
的斜率之积为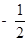 .
.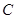 的方程;
的方程; 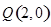 , 过点
, 过点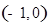 的直线
的直线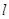 交
交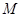 、
、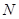 两点, 若对满足条件的任意直线
两点, 若对满足条件的任意直线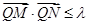 恒成立, 求
恒成立, 求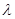 的最小值.
的最小值. 的参数方程为
的参数方程为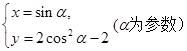 ,曲线
,曲线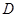 的极坐标方程为
的极坐标方程为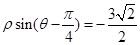 .
. 到点
到点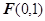 的距离与点
的距离与点 轴的距离的差等于1.(I)求动点
轴的距离的差等于1.(I)求动点 的方程;(II)过点
的方程;(II)过点 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线 ,设
,设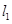 与轨迹
与轨迹 ,
, 与轨迹
与轨迹 ,求
,求 的最小值.
的最小值.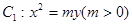 的准线与
的准线与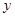 轴交于
轴交于 ,焦点为
,焦点为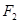 ,若椭圆
,若椭圆 以
以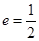 .
. 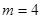 时,求椭圆
时,求椭圆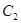 的方程;
的方程; 与直线
与直线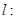
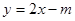 及
及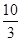 ,求抛物线
,求抛物线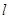 的方程.
的方程.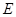 :
: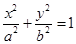 (
( )过点
)过点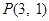 ,其左、右焦点分别为
,其左、右焦点分别为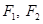 ,且
,且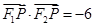 .
. 是直线
是直线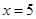 上的两个动点,且
上的两个动点,且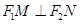 ,则以
,则以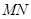 为直径的圆
为直径的圆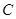 是否过定点?请说明理由.
是否过定点?请说明理由.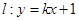 过定点
过定点 ,动点
,动点 满足
满足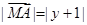 ,动点
,动点 .
.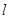 与
与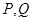 两点,以
两点,以 .
.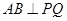 ;②若直线
;②若直线 与
与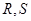 两点,求四边形
两点,求四边形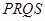 面积的最大值.
面积的最大值.