题目内容
已知直线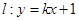 过定点
过定点 ,动点
,动点 满足
满足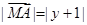 ,动点
,动点 的轨迹为
的轨迹为 .
.
(Ⅰ)求 的方程;
的方程;
(Ⅱ)直线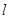 与
与 交于
交于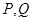 两点,以
两点,以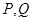 为切点分别作
为切点分别作 的切线,两切线交于点
的切线,两切线交于点 .
.
①求证: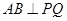 ;②若直线
;②若直线 与
与 交于
交于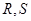 两点,求四边形
两点,求四边形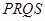 面积的最大值.
面积的最大值.
(1)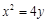 (2) 根据直线斜率互为负倒数来得到证明,当且仅当
(2) 根据直线斜率互为负倒数来得到证明,当且仅当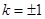 时,四边形
时,四边形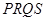 面积的取到最小值
面积的取到最小值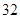 。
。
解析试题分析:(I)由题意知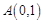 ,设
,设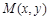
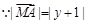
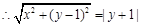 化简得
化简得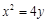 3分
3分
(Ⅱ)①设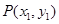 ,
, ,
,
由 消去
消去 ,得
,得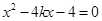 ,显然
,显然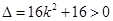 .
.
所以 ,
,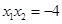
由 ,得
,得 ,所以
,所以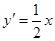 ,
,
所以,以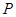 为切点的切线的斜率为
为切点的切线的斜率为 ,
,
所以,以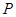 为切点的切线方程为
为切点的切线方程为 ,又
,又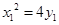 ,
,
所以,以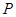 为切点的切线方程为
为切点的切线方程为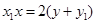 ……(1)
……(1)
同理,以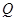 为切点的切线方程为
为切点的切线方程为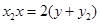 ……(2)
……(2)
(2)-(1)并据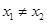 得点
得点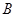 的横坐标
的横坐标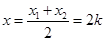 ,
,
代入(1)易得点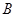 的纵坐标
的纵坐标 ,所以点
,所以点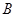 的坐标为
的坐标为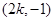
当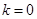 时,显然
时,显然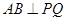
当 时,
时, ,从而
,从而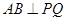 8分
8分
②由已知,显然直线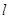 的斜率不为0,由①知
的斜率不为0,由①知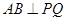 ,所以
,所以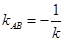 ,
,
则直线 的方程为
的方程为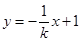 ,
,
设设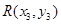 ,
,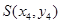 ,
,
由 消去
消去 ,得
,得 ,显然
,显然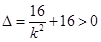 ,
,
所以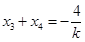 ,
,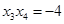 .
.
又
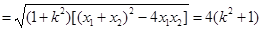
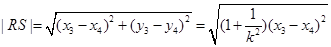

因为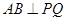 ,所以
,所以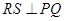 ,
,
所以,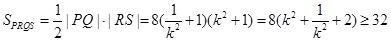 ,
,
当且仅当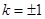 时,四边形
时,四边形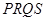 面积的取到最小值
面积的取到最小值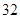 13分
13分
考点:直线与抛物线的位置关系
点评:解决的关键是借助于向量的模来表示得到轨迹方程,并联立方程组来得到弦长公式,进而得到面积的表示,属于中档题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的顶点为坐标原点
的顶点为坐标原点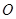 ,焦点
,焦点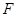 在
在 轴上,准线
轴上,准线 与圆
与圆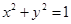 相切.
相切.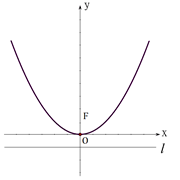
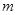 和抛物线
和抛物线 ,命题P:“若直线
,命题P:“若直线 ,则
,则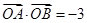 ”,请判断命题P的真假,并证明。
”,请判断命题P的真假,并证明。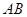 的两个端点
的两个端点 、
、 分别分别在
分别分别在 轴、
轴、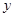 轴上滑动,
轴上滑动,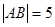 ,点
,点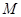 是
是 ,点
,点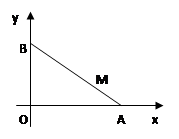
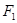 为点
为点 为右焦点,过
为右焦点,过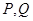 两点,求
两点,求 的最大值,并求此时直线
的最大值,并求此时直线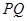 的方程.
的方程. 的椭圆
的椭圆 (a>b>0)的左、右焦点,直线
(a>b>0)的左、右焦点,直线 :x=-
:x=-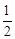 将线段F1F2分成两段,其长度之比为1 : 3.设A,B是C上的两个动点,线段AB的中点M在直线l上,线段AB的中垂线与C交于P,Q两点.
将线段F1F2分成两段,其长度之比为1 : 3.设A,B是C上的两个动点,线段AB的中点M在直线l上,线段AB的中垂线与C交于P,Q两点.
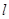 经过抛物线
经过抛物线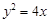 的焦点F,且与抛物线相交于A、B两点.
的焦点F,且与抛物线相交于A、B两点.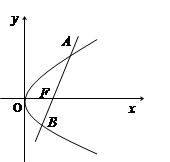
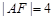 ,求点A的坐标;
,求点A的坐标;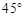 ,求线段AB的长.
,求线段AB的长.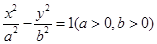 与椭圆
与椭圆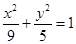 有相同的焦点
有相同的焦点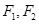 ,且该双曲线
,且该双曲线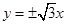 .
.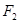 作斜率不为零的直线与此双曲线的左,右两支分别交于点
作斜率不为零的直线与此双曲线的左,右两支分别交于点 、
、 ,
,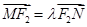 ,当
,当 轴上的点
轴上的点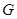 满足
满足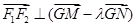 时,求点
时,求点 ,在抛物线上任意画一个点
,在抛物线上任意画一个点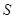 ,度量点
,度量点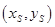 ,如图.
,如图.
 时,
时,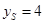 ,试求抛物线
,试求抛物线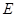 的方程;
的方程;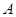 ,焦点为
,焦点为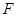 ,构造直线
,构造直线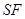 交抛物线
交抛物线 ,构造直线
,构造直线 、
、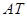 分别交准线于
分别交准线于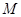 、
、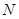 两点,构造直线
两点,构造直线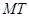 、
、 .经观察得:沿着抛物线
.经观察得:沿着抛物线 .请你证明这一结论.
.请你证明这一结论. 
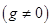 ”,其余条件不变,发现“
”,其余条件不变,发现“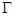 的方程为
的方程为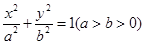 ,点P的坐标为(-a,b).
,点P的坐标为(-a,b). ,求点
,求点 的坐标;
的坐标;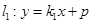 交椭圆
交椭圆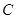 、
、 两点,交直线
两点,交直线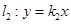 于点
于点 .若
.若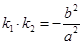 ,证明:
,证明: 的中点;
的中点;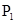 、
、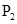 满足
满足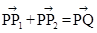 ,写出求作点
,写出求作点