题目内容
20.某食品店为了了解气温对销售量的影响,随机记录了该店1月份中5天的日销售量y(单位:千克)与该地当日最低气温x(单位:°C)的数据,如下表:| x | 2 | 5 | 8 | 9 | 11 |
| y | 12 | 10 | 8 | 8 | 7 |
(2)判断y与x之间是正相关还是负相关;若该地1月份某天的最低气温为6°C,请用所求回归方程预测该店当日的销售量;
(3)设该地1月份的日最低气温X~N(μ,σ2),其中μ近似为样本平均数$\overline x$,σ2近似为样本方差s2,求P(3.8<X<13.4).
附:①回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中,$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}{y}_{i})-n\overline{x\overline{y}}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
②$\sqrt{10}$≈3.2,$\sqrt{3.2}$≈1.8.若X~N(μ,σ2),则P(μ-σ<X<μ+σ)=0.6826,P(μ-2σ<X<μ+2σ)=0.9544.
分析 (1)利用回归系数公式计算回归系数,得出回归方程;
(2)根据$\widehat{b}$的符号判断,把x=6代入回归方程计算预测值;
(3)求出样本的方差,根据正态分布知识得P(3.8<X<13.4)=P(3.8<X<10.2)+P(10.2<X<13.4).
解答 解:(1)$\overline{x}$=$\frac{1}{5}$×(2+5+8+9+11)=7,$\overline{y}$=$\frac{1}{5}$×(12+10+8+8+7)=9.
$\sum_{i=1}^{5}$(xi-$\overline{x}$)(yi-$\overline{y}$)=4+25+64+81+121=295,
$\sum_{i=1}^{5}$xiyi=24+50+64+72+77=287,
∴$\widehat{b}$=$\frac{287-5×7×9}{295-5×72}$=-0.56,
$\widehat{a}$=9-(-0.56)×7=12.92.
∴回归方程为:$\widehat{y}$=-0.56x+12.92.
(2)∵$\widehat{b}$=-0.56<0,∴y与x之间是负相关.
当x=6时,$\widehat{y}$=-0.56×6+12.92=9.56.
∴该店当日的营业额约为9.56千元.
(3)样本方差s2=$\frac{1}{5}$×[25+4+1+4+16]=10,
∴最低气温X~N(7,10),
∴P(3.8<X<10.2)=0.6826,P(0,6<X<13.4)=0.9544,
∴P(10.2<X<13.4)=$\frac{1}{2}$(0.9544-0.6826)=0.1359.
∴P(3.8<X<13.4)=P(3.8<X<10.2)+P(10.2<X<13.4)=0.6826+0.1359=0.8185.
点评 本题考查了线性回归方程的求解,数值预测,正态分布,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
| A. | A12 | B. | A13 | C. | A14 | D. | A15 |
| A. | $\sqrt{29}$-$\sqrt{13}$ | B. | 5+$\sqrt{13}$ | C. | 2$\sqrt{7}$+$\sqrt{13}$ | D. | $\sqrt{29}$+$\sqrt{13}$ |
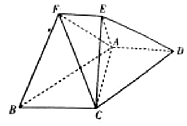 已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.
已知多面体ABCDEF中,四边形ABCD为平行四边形,AD⊥平面AEC,且$AC=\sqrt{2}$,AE=EC=1,AD=2EF,EF∥AD.