题目内容
直三棱柱ABC-A′B′C′中,AC=BC=AA′,∠ACB=90°,
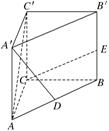 D、E分别为AB、BB′的中点.
D、E分别为AB、BB′的中点.
(1)求证:CE⊥A′D;
(2)求异面直线CE与AC′所成角的余弦值.
解:(1)证明:设  =a,
=a,  =b,
=b,  =c,
=c,
 根据题意,|a|=|b|=|c|且a·b=b·c=c·a=0,
根据题意,|a|=|b|=|c|且a·b=b·c=c·a=0,
∴  =b+
=b+ c,
c,  =-c+
=-c+ b-
b- a.
a.
∴  ·
·  =-
=- c2+
c2+ b2=0,
b2=0,
∴  ⊥
⊥ ,即CE⊥A′D.
,即CE⊥A′D.
(2)  =-a+c,∴|
=-a+c,∴|  |=
|= |a|,|
|a|,|  |=
|= |a|.
|a|.
 ·
· =(-a+c)·(b+
=(-a+c)·(b+ c)=
c)= c2=
c2= |a|2,
|a|2,
∴cos〈  ,
, 〉=
〉= =
= .
.
即异面直线CE与AC′所成角的余弦值为 .
.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
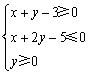 ,则
,则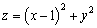 的最小值是 .
的最小值是 .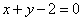 相切的圆的方程为
相切的圆的方程为 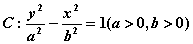 的离心率为
的离心率为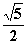 ,则C的渐近线方程为( )
,则C的渐近线方程为( )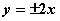 B.
B.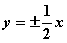 C.
C.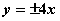 D.
D.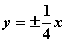
 , 则
, 则 互为相反数”的逆命题;
互为相反数”的逆命题; 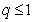 ,则
,则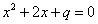 有实根”的逆否命题;
有实根”的逆否命题;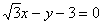 的倾斜角是( )
的倾斜角是( )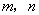 ,两个平面
,两个平面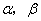 .下面四个命题中不正确的是( )
.下面四个命题中不正确的是( )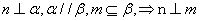 B.
B.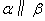 ,
,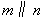 ,
,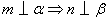 ;
;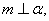
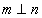 ,
,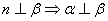 D.
D. ;
; 
 的解集是 ( )
的解集是 ( ) B
B  C
C  D
D 
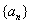 的前
的前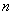 项和为
项和为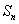 ,
,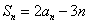 (
(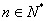 ).
). 是等比数列,求出数列
是等比数列,求出数列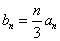 ,求数列
,求数列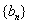 的前
的前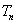 ;
;