题目内容
2.如图,C,D是以AB为直径的圆上的两点,AB=2AD=2$\sqrt{3}$,AC=BC,F是AB上的一点,且AF=$\frac{1}{3}$AB,将圆沿AB折起,使点C在平面ABD的正投影E在线段BD上,已知CE=$\sqrt{2}$,平面EFMN分别交AC、DC于点M、N.(1)求证:AD⊥平面BCE;
(2)求证:AD∥MN;
(3)求三棱锥A-CFD的体积.
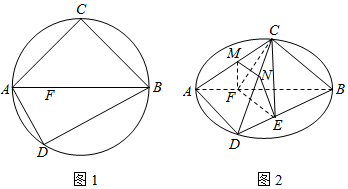
分析 (1)依题AD⊥BD,CE⊥AD,由此能证明AD⊥平面BCE;
(2)由已知得BE=2,BD=3.从而AD∥EF,由此能证明AD∥平面CEF;
(3)由VA-CFD=VC-AFD,利用等积法能求出三棱锥A-CFD的体积.
解答  (1)证明:依题意,AD⊥BD
(1)证明:依题意,AD⊥BD
∵CE⊥平面ABD,∴CE⊥AD,
∵BD∩CE=E,
∴AD⊥平面BCE;
(2)证明:Rt△BCE中,CE=$\sqrt{2}$,BC=$\sqrt{6}$,∴BE=2,
Rt△ABD中,AB=2$\sqrt{3}$,AD=$\sqrt{3}$,∴BD=3.
∴$\frac{BF}{BA}=\frac{BE}{BD}=\frac{2}{3}$,则AD∥EF,
∵AD?平面ADC,EF?平面ADC,
∴EF∥平面ADC.
又EF?平面EFMN,且平面EFMN∩平面ADC=MN,
∴EF∥MN,则AD∥MN;
(3)解:由(2)知AD∥EF,AD⊥ED,
且ED=BD-BE=1,
∴F到AD的距离等于E到AD的距离为1.
∴S△FAD=$\frac{1}{2}$×$\sqrt{3}×1=\frac{\sqrt{3}}{2}$.
∵CE⊥平面ABD,
∴VA-CFD=VC-AFD=$\frac{1}{3}$S△FAD•CE=$\frac{1}{3}$×$\frac{\sqrt{3}}{2}×\sqrt{2}$=$\frac{\sqrt{6}}{6}$.
点评 本题考查直线与平面垂直的判定,直线与平面平行的判定,求棱锥的体积,求解本题的关键是创造出线面垂直、线面平行的条件,熟知相关的定理是求解这一类题的保证,属中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC,EA⊥EB.
如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC,EA⊥EB.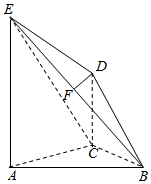 在如图所示的几何体中,平面ACDE⊥平面ABC,CD∥AE,F是BE的中点,∠ACB=90°,AE=2CD=2,AC=BC=1,BE=$\sqrt{6}$.
在如图所示的几何体中,平面ACDE⊥平面ABC,CD∥AE,F是BE的中点,∠ACB=90°,AE=2CD=2,AC=BC=1,BE=$\sqrt{6}$.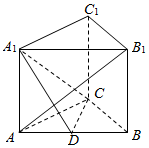 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,AB1⊥平面A1CD,AC⊥BC,D为AB中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,AB1⊥平面A1CD,AC⊥BC,D为AB中点.