题目内容
7.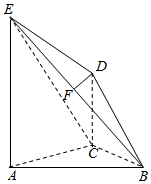 在如图所示的几何体中,平面ACDE⊥平面ABC,CD∥AE,F是BE的中点,∠ACB=90°,AE=2CD=2,AC=BC=1,BE=$\sqrt{6}$.
在如图所示的几何体中,平面ACDE⊥平面ABC,CD∥AE,F是BE的中点,∠ACB=90°,AE=2CD=2,AC=BC=1,BE=$\sqrt{6}$.(1)求证:DF∥平面ABC;
(2)求证:DF⊥平面ABE;
(3)求三棱锥D-BCE的体积.
分析 (1)取AB中点M,利用三角形的中位线的性质可得四边形CDFM为平行四边形,从而得到DF∥CM,再由线面平行的判定得到DF∥平面ABC;
(2)由已知求解直角三角形证明AE⊥AB,由面面垂直的性质可得AC⊥BC,再由线面垂直的判定得到AE⊥平面ABC,从而AE⊥CM.在△ABC中,由AC=BC,M为AB中点,
得CM⊥AB,进一步得到CM⊥平面ABE.结合(1)知DF∥CM,则DF⊥平面ABE;
(3)由(2)可知BC为三棱锥B-CDE的高,然后利用等积法求得三棱锥D-BCE的体积.
解答 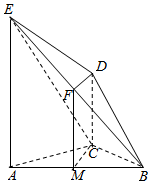 证明:(1)设M为AB中点,连结FM,CM
证明:(1)设M为AB中点,连结FM,CM
在△ABE中,又F为BE中点,∴$FM∥AE,FM=\frac{1}{2}AE$.
又∵CD∥AE,且$CD=\frac{1}{2}AE$,
∴CD∥FM,CD=FM.
则四边形CDFM为平行四边形.
故DF∥CM,又DF?平面ABC,CM?平面ABC,
∴DF∥平面ABC;
(2)在Rt△ABC中,AC=BC=1,∴$AB=\sqrt{2}$.
在△ABE中,AE=2,$BE=\sqrt{6}$,$AB=\sqrt{2}$.
∵BE2=AE2+AB2.
∴△ABE为直角三角形.
∴AE⊥AB.
又∵平面ACDE⊥平面ABC,平面ACDE∩平面ABC=AC,且∠ACB=90°,
∴AC⊥BC.
故BC⊥平面ACDE.
即BC⊥AE.
∵BC∩AB=B,
∴AE⊥平面ABC,而CM?平面ABC,
故AE⊥CM.
在△ABC中,∵AC=BC,M为AB中点,
∴CM⊥AB.AE∩AB=A,
∴CM⊥平面ABE.
由(1)知 DF∥CM,
∴DF⊥平面ABE;
(3)由(2)可知BC⊥平面ACDE,
∴BC为三棱锥B-CDE的高,
∴VD-BCF=VB-CDE=$\frac{1}{3}{S}_{△CDE}•BC=\frac{1}{3}×\frac{1}{2}×1×1×1=\frac{1}{6}$.
点评 本题考查直线与平面平行的判定、直线与平面垂直的判定,训练了利用等积法求多面体的体积,考查空间想象能力和思维能力,是中档题.

 名校课堂系列答案
名校课堂系列答案| A. | {x|-1≤x≤3} | B. | {x|-1≤x<3} | C. | {-1,0,1,2,3} | D. | {-1,0,1,2} |
| 时间 | 11日 | 12日 | 13日 | 14日 | 15日 | 16日 | 17日 | 18日 | 19日 | 20日 |
| AQI | 149 | 143 | 251 | 254 | 138 | 55 | 69 | 102 | 243 | 269 |
(Ⅱ)一外地游客在12月来济南旅游,想连续游玩两天,求适合旅游的概率.
 函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)解析式f(x)=2sin(2x-$\frac{π}{3}$).
函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)解析式f(x)=2sin(2x-$\frac{π}{3}$).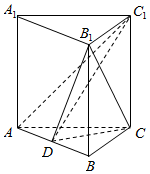 如图,在三棱柱ABC-A1B1C1中,AC=4,BC=3,AB=B1C=5,点D是线段AB的中点,四边形ACC1A1为正方形.
如图,在三棱柱ABC-A1B1C1中,AC=4,BC=3,AB=B1C=5,点D是线段AB的中点,四边形ACC1A1为正方形. 如图,在四棱锥S-ABCD中,已知底面ABCD为直角梯形,其中AD∥BC,∠BAD=90°,SA⊥底面ABCD,$SA=AB=BC=2,tan∠SDA=\frac{2}{3}$.
如图,在四棱锥S-ABCD中,已知底面ABCD为直角梯形,其中AD∥BC,∠BAD=90°,SA⊥底面ABCD,$SA=AB=BC=2,tan∠SDA=\frac{2}{3}$.