题目内容

(1)求双曲线的标准方程;
(2)设F1和F2是这双曲线的左、右焦点,点P在这双曲线上,且|PF1|·|PF2|=32,求
∠F1PF2的大小
(1)
 (2)
(2)
(1)由渐近线方程知双曲线中心在原点,且渐近线上横坐标为 的点
的点 的纵坐标绝对值为
的纵坐标绝对值为
 ∴双曲线的焦点在
∴双曲线的焦点在 轴上,设方程
轴上,设方程 ………………3分
………………3分
∵双曲线过点 ①
①
又 ②
②
由①②得 ,∴所求的双曲线方程为
,∴所求的双曲线方程为 …………6分
…………6分
(2)证|PF1|=d1,|PF2|=d2,则d1·d2=32
又由双曲线的几何性质知|d1-d2|=2a=6…………8分
 即有
即有 ………………10分
………………10分
又|F1F2|="2c=10 "
△PF1F2是直角三角形, ………………………………12分
………………………………12分
 的点
的点 的纵坐标绝对值为
的纵坐标绝对值为
 ∴双曲线的焦点在
∴双曲线的焦点在 轴上,设方程
轴上,设方程 ………………3分
………………3分∵双曲线过点
 ①
①又
 ②
②由①②得
 ,∴所求的双曲线方程为
,∴所求的双曲线方程为 …………6分
…………6分(2)证|PF1|=d1,|PF2|=d2,则d1·d2=32
又由双曲线的几何性质知|d1-d2|=2a=6…………8分
 即有
即有 ………………10分
………………10分又|F1F2|="2c=10 "

△PF1F2是直角三角形,
 ………………………………12分
………………………………12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
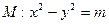 ,
,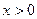 ,
,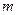 为正常数.直线
为正常数.直线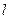 与曲线
与曲线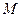 的实轴不垂直,且依次交直线
的实轴不垂直,且依次交直线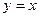 、曲线
、曲线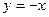 于
于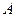 、
、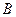 、
、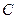 、
、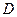 4个点,
4个点,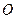 为坐标原点.
为坐标原点.
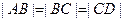 ,求证:
,求证: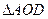 的面积为定值;
的面积为定值;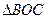 的面积等于
的面积等于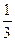 ,求证:
,求证: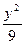 -
-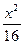 =-1上的点M到点A(5,0)的距离为25,则M到点B(-5,0)的距离是___________________.
=-1上的点M到点A(5,0)的距离为25,则M到点B(-5,0)的距离是___________________. ,则a+b的值为( )
,则a+b的值为( )
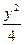 =1有共同渐近线,且过点(2,2)的双曲线方程是( )
=1有共同渐近线,且过点(2,2)的双曲线方程是( )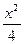 -y2="1"
-y2="1"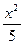 -
-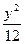 =1
=1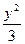 ="1"
="1"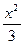 -
-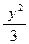 =1上有一点P,使得|PA|+
=1上有一点P,使得|PA|+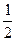 |PF|最小,则点P的坐标是_______________.
|PF|最小,则点P的坐标是_______________.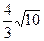
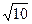
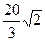

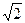 +1
+1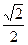 +1
+1 的渐近线与抛物线
的渐近线与抛物线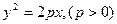 交于三个不同的点O,A,B,(其中0是坐标原点),若
交于三个不同的点O,A,B,(其中0是坐标原点),若 为等边三角形,则双曲线的离心率为
为等边三角形,则双曲线的离心率为