题目内容
过双曲线的一个焦点F1且垂直于实轴的弦PQ,若F2是另一个焦点,且∠PF2Q=90°,则此双曲线的离心率为( )
A.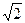 +1 +1 | B.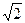 | C.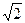 -1 -1 | D.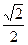 +1 +1 |
A
设双曲线方程为 =1.当x=-c时|y|=
=1.当x=-c时|y|= ,由题意知
,由题意知
 =2c
=2c b2=2ac
b2=2ac c2-a2-2ac=0
c2-a2-2ac=0 e2-2e-1=0
e2-2e-1=0 e=
e=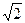 +1.
+1.
 =1.当x=-c时|y|=
=1.当x=-c时|y|= ,由题意知
,由题意知 =2c
=2c b2=2ac
b2=2ac c2-a2-2ac=0
c2-a2-2ac=0 e2-2e-1=0
e2-2e-1=0 e=
e=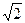 +1.
+1.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 =1(a>b>0)的两条渐近线的夹角为α,则它的离心率是( )
=1(a>b>0)的两条渐近线的夹角为α,则它的离心率是( )

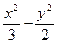 =1上截得弦长为4,其斜率为2,则直线l在y轴上的截距是_____________.
=1上截得弦长为4,其斜率为2,则直线l在y轴上的截距是_____________.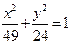 有共同的焦点,且以
有共同的焦点,且以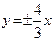 为渐近线.
为渐近线.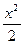 -y
-y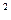 =1有公共渐近线的双曲线方程是( )
=1有公共渐近线的双曲线方程是( )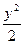 -
-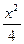 ="1"
="1"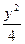 =1
=1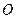 ,焦点在
,焦点在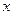 轴上,两条渐近线分别为
轴上,两条渐近线分别为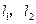 ,经过右焦点
,经过右焦点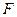 垂直于
垂直于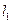 的直线分别交
的直线分别交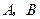 两点.已知
两点.已知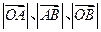 成等差数列,且
成等差数列,且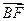 与
与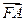 同向.
同向.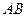 被双曲线所截得的线段的长为4,求双曲线的方程.
被双曲线所截得的线段的长为4,求双曲线的方程.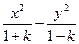 =1表示双曲线,则k的取值范围是( )
=1表示双曲线,则k的取值范围是( )