��Ŀ����
13����֪$D=\left\{{\left.{��{x��y}��}\right|\left\{\begin{array}{l}x+y-2��0\\ x-y+2��0\\ 3x-y+6��0\end{array}\right.}\right\}$�����������ĸ����⣺P1��?��x��y����D��x+y��0��
P2��?��x��y����D��2x-y+1��0��
${P_3}��?��{x��y}����D��\frac{y+1}{x-1}��-4$��
${P_4}��?��{x��y}����D��{x^2}+{y^2}��2$��
������������ǣ�������
| A�� | P1��P2 | B�� | P2��P3 | C�� | P3��P4 | D�� | P2��P4 |
���� ����Լ���������ǵĿ���������Ŀ�꺯���ļ������壬�����Χ���ж�ѡ������ɣ�
��� �⣺$D=\left\{{\left.{��{x��y}��}\right|\left\{\begin{array}{l}x+y-2��0\\ x-y+2��0\\ 3x-y+6��0\end{array}\right.}\right\}$�Ŀ�������ͼ��
p1��A��-2��0���㣬-2+0=-2��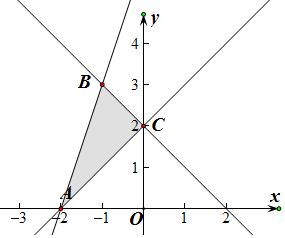 x+y����СֵΪ-2��
x+y����СֵΪ-2��
��?��x��y����D��x+y��0Ϊ�����⣻
p2��B��-1��3���㣬-2-3+1=-4��
A��-2��0����-4-0+1=-3��C��0��2����0-2+1=-1��
��?��x��y����D��2x-y+1��0Ϊ�����⣻
p3��C��0��2���㣬$\frac{2+1}{0-1}$=-3��
��?��x��y����D��$\frac{y+1}{x-1}$��-4Ϊ�����⣻
p4����-1��1���㣬x2+y2=2��
��?��x��y����D��x2+y2��2Ϊ�����⣮
�ɵ�ѡ��p2��p4��ȷ��
��ѡ��D��
���� ���⿼�����Թ滮�Ľ��Ӧ�ã��������ٵ��жϣ���ȷ�����������Լ�Ŀ�꺯���ļ��������ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
3�����������������ҹ��Ŵ���ѧ�ɾ͵Ľܳ��������ǡ��㾭ʮ�顱������Ҫ��һ�֣��ǵ�ʱ�������������Ч��Ӧ�����֣����ij��ֱ�־�й��Ŵ���ѧ�γ�����������ϵ�����С�������л�������������⣬������Ի�����ҳ�ʸ��ʸ���Գˣ���֮������һ��������ǣ�����������㹫ʽΪ���������=$\frac{1}{2}$���ҡ�ʸ+ʸ��ʸ������������Բ�������Ϊ���ﻡ������Բ���Ķ˵�Ϊ�˵���߶Σ����Ϊ���ﻡ��Χ�ɵ�ƽ��ͼ�Σ���ʽ�С��ҡ�ָ���ǻ����ҵij�����ʸ�����ڻ��ﻡ����Բ�İ뾶��Բ�ĵ������ҵľ���֮�����һ������ҳ�AB����6�ף��仡����ԲΪԲO��������������������㹫ʽ��øû�������Ϊ$\frac{7}{2}$ƽ���ף���cos��AOB=��������
| A�� | $\frac{1}{25}$ | B�� | $\frac{3}{25}$ | C�� | $\frac{1}{5}$ | D�� | $\frac{7}{25}$ |
4����֪iΪ������λ������z����z=i��z-i��������z����Ӧ�ĵ�Z�ڣ�������
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
1����ֱ��y=x�ϴ��ڵ㣨x��y������Լ������$\left\{\begin{array}{l}x+y-4��0\\ x-2y-3��0\\ x��m\end{array}\right.$����ʵ��m�����ֵΪ��������
| A�� | -1 | B�� | 1 | C�� | $\frac{3}{2}$ | D�� | 2 |
3����֪����p��ֱ��l1��2ax+y+1=0��l2��x+2ay+2=0��l1��l2�ij�ֲ���Ҫ������a=$\frac{1}{2}$������q��?x�ʣ�0���У���sinx+$\frac{1}{sinx}$��2���������ж���ȷ���ǣ�������
| A�� | ����p��q�Ǽ����� | B�� | ����p��q�������� | ||
| C�� | ����p�ţ��Vq���Ǽ����� | D�� | ����p�ģ��Vq���������� |