题目内容
解不等式组
．
|
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：先求一元二次不等式的解x≥3或x≤-2，再求绝对值不等式的解-2＜x＜6，再求它们的交集．
解答：
解：不等式x2-x-6≥0 化为（x-3）（x+2）≥0，解得x≥3或x≤-2，
解不等式|x-2|＜4，化为-4＜x-2＜4，解得-2＜x＜6，
∴不等式的解集为{x|x≥3或x≤-2}∩{x|-2＜x＜6}={x|3≤x＜6}．
解不等式|x-2|＜4，化为-4＜x-2＜4，解得-2＜x＜6，
∴不等式的解集为{x|x≥3或x≤-2}∩{x|-2＜x＜6}={x|3≤x＜6}．
点评：本题考查了一元二次不等式的解法、含绝对值不等式的解法、不等式组的解法，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若m＞1，则方程
+
=1表示（ ）
| x2 |
| m-1 |
| y2 |
| m2-1 |
| A、焦点在x轴上的椭圆 |
| B、焦点在y轴上的椭圆 |
| C、焦点在x轴上的双曲线 |
| D、焦点在y轴上的双曲线 |
若抛物线y2=2px，（p＞0）上一点P（2，y0）到其准线的距离为4，则抛物线的标准方程为（ ）
| A、y2=4x |
| B、y2=6x |
| C、y2=8x |
| D、y2=10x |
坚持锻炼一小时，健康成长每一天．某校为调查高中学生在校参加体育活动的时间，随机抽取了100名高中学生进行调查，其中女学生有55名．上面是根据调查结果绘制的学生日均体育锻炼时间的频率分布直方图：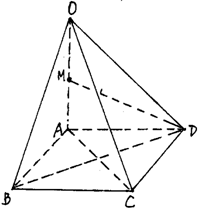
如图，在四棱锥O-ABCD中，底面ABCD是边长为1的正方形，OA⊥底面ABCD，OA=2，M为OA中点．