题目内容
6.函数f(x)是定义在R上的减函数,且f(x)>0恒成立,若对任意的x,y∈R,都有f(x+y)=f(x)•g(x).(1)求f(0)的值;
(2)若f(-1)=3,解不等式$\frac{f({x}^{2})•f(10)}{f(7x)}$≤9.
分析 (1)令x=y=0,f(0)=f2(0),f(x)>0,f(0)=1;
(2)原不等式等价于f(x2)f(10)≤9f(7x )⇒f(x2)f(10)≤f(7x)f(-2)⇒f(x2+10)≤f(7x-2)又f(x)是定义在R上的减函数,x2+10≥7x-2即可.
解答 解(1)令x=y=0,∴f(0)=f2(0),∵f(x)>0,∴f(0)=1,…(3分)
(2)∵f(x)>0,∴$\frac{{f({x^2})f(10)}}{f(7x)}≤9$,得f(x2)f(10)≤9f(7x),…(4分)
∵f(-1)=3,∴9=3×3=f(-1)f(-1)=f(-2),…(6分)
∴f(x2)f(10)≤f(7x)f(-2)可化为,f(x2+10)≤f(7x-2),…(8分)
又f(x)是定义在R上的减函数,∴x2+10≥7x-2,…(10分)
解得,x≤3,x≥4,…(11分)
即原不等式的解集为(-∞,3]∪[4,+∞)…(12分)
点评 本题考查了抽象函数的赋值法,及抽象函数不等式的解法,关键是根据单调性及定义域进行转化,属于基础题.

练习册系列答案
相关题目
16.若复数z=$\frac{4-2ai}{1-i}$(a∈R)的实部为1,则z的虚部为( )
| A. | 1 | B. | 3 | C. | -1 | D. | -3 |
14.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$两渐近线的夹角θ满足$sinθ=\frac{4}{5}$,焦点到渐近线的距离d=1,则该双曲线的焦距为( )
| A. | $\sqrt{5}$ | B. | $\frac{\sqrt{5}}{2}$或$\sqrt{5}$ | C. | $\sqrt{5}$或$2\sqrt{5}$ | D. | 以上都不是 |
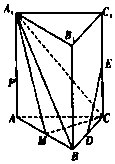 如图,正三棱柱ABC-A1B1C1中,D,E,M分别是线段BC,CC1,AB的中点,AA1=2AB=4.
如图,正三棱柱ABC-A1B1C1中,D,E,M分别是线段BC,CC1,AB的中点,AA1=2AB=4.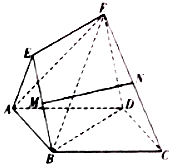 如图5所示,四边形ABCD是边长为2的正方形,四边形BDFE是平行四边形,点M,N分别是BE,CF的中点.
如图5所示,四边形ABCD是边长为2的正方形,四边形BDFE是平行四边形,点M,N分别是BE,CF的中点.