题目内容
已知向量
=(1,k),
=(2,2),且
+
与
共线,那么k的值为( )
| a |
| b |
| a |
| b |
| a |
| A、1 | B、2 | C、3 | D、4 |
考点:平面向量共线(平行)的坐标表示
专题:平面向量及应用
分析:由向量的坐标加法运算求得
+
的坐标,然后直接利用向量共线的坐标表示列式求解k的值.
| a |
| b |
解答:
解:∵
=(1,k),
=(2,2),
∴
+
=(3,k+2),
又
+
与
共线,
∴1×(k+2)-3k=0,
解得:k=1.
故选:A.
| a |
| b |
∴
| a |
| b |
又
| a |
| b |
| a |
∴1×(k+2)-3k=0,
解得:k=1.
故选:A.
点评:平行问题是一个重要的知识点,在高考题中常常出现,常与向量的模、向量的坐标表示等联系在一起,要特别注意垂直与平行的区别.若
=(a1,a2),
=(b1,b2),则
⊥
?a1a2+b1b2=0,
∥
?a1b2-a2b1=0,是基础题.
| a |
| b |
| a |
| b |
| a |
| b |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若集合A={x|x2-7x+10<0},集合B={x|
<2x<8},则A∩B=( )
| 1 |
| 2 |
| A、(-1,3) |
| B、(-1,5) |
| C、(2,5) |
| D、(2,3) |
设函数f(x)=(x2-8x+c1)(x2-8x+c2)(x2-8x+c3) (x2-8x+c4),集合M={x|f(x)=0}={x1,x2…,x7}⊆N+,设c1≥c2≥c3≥c4,则c1-c4( )
| A、9 | B、8 | C、7 | D、6 |
已知R是实数集,集合P={x|y=ln(x2+2014x-2015)},Q={y|y=
},则(∁RP)∪Q( )
| -x2+2x+3 |
| A、(0,1] |
| B、[0,1] |
| C、(-2015,1] |
| D、[-2015,2] |
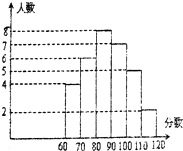 某中学部分学生参加市数学竞赛取得了优异成绩,指导老师统计了所有参赛同学的成绩(成绩都为整数,满分120分),并且绘制了“频数分布直方图”(如图)如果90分以上(含90分)获奖,那么该校参赛学生的获奖率为( )
某中学部分学生参加市数学竞赛取得了优异成绩,指导老师统计了所有参赛同学的成绩(成绩都为整数,满分120分),并且绘制了“频数分布直方图”(如图)如果90分以上(含90分)获奖,那么该校参赛学生的获奖率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
从0,1,2,3,4,5这六个数字中,任取两个不同数字相加,其和为偶数的不同取法的种数有( )
| A、30 | B、20 | C、10 | D、6 |