题目内容
7.已知随机变量ξ~B(3,$\frac{1}{2}$),则E(ξ)=( )| A. | 3 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
分析 利用二项分布列的性质即可得出.
解答 解:∵随机变量ξ~B(3,$\frac{1}{2}$),则E(ξ)=3×$\frac{1}{2}$=$\frac{3}{2}$.
故选:C.
点评 本题考查了二项分布列的性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
2.设z=x+2y,其中实数x,y满足$\left\{\begin{array}{l}{x+y≥0}\\{x-y≥0}\\{0≤x≤a}\end{array}\right.$,若z的最小值为-1,则z的最大值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 2 |
19.某设备的使用年数x与所支出的维修总费用y的统计数据如下表:
根据上标可得回归直线方程为$\widehat{y}$=1.3x+$\widehat{a}$,若该设备维修总费用超过12万元,据此模型预测该设备最多可使用9年.
| 使用年数x(单位:年) | 2 | 3 | 4 | 5 | 6 |
| 维修费用y(单位:万元) | 1.5 | 4.5 | 5.5 | 6.5 | 7.0 |
 满足
满足 则
则 的最大值等于( )
的最大值等于( ) B.
B. C.
C. D.
D.
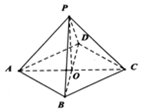 如图,在边长为2的菱形ABCD中,∠BAD=60°,O为AC的中点,点P为平面ABCD外一点,且平面PAC⊥平面ABCD,PO=1,PA=2.
如图,在边长为2的菱形ABCD中,∠BAD=60°,O为AC的中点,点P为平面ABCD外一点,且平面PAC⊥平面ABCD,PO=1,PA=2. 某几何体的三视图如图所示,则这个几何体的体积为$\frac{20}{3}$.
某几何体的三视图如图所示,则这个几何体的体积为$\frac{20}{3}$.