题目内容
11.已知双曲线C2与椭圆C1:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1具有相同的焦点,则两条曲线相交四个交点形成四边形面积最大时双曲线C2的离心率为$\sqrt{2}$.分析 求解面积最大值时的点的坐标,利用焦点坐标,转化求解双曲线的离心率即可.
解答 解:双曲线C2与椭圆C1:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1具有相同的焦点,可得c=1,
两条曲线相交四个交点形成四边形面积最大,设在第一象限的交点为:(m,n),可得S=4mn,
$1=\frac{{m}^{2}}{4}+\frac{{n}^{2}}{3}$≥2$\sqrt{\frac{{m}^{2}}{4}•\frac{{n}^{2}}{3}}$=$\frac{\sqrt{3}}{3}mn$,当且仅当$\sqrt{3}m=2n$时,mn≤$\sqrt{3}$,此时四边形的面积取得最大值,
解得m=$\sqrt{2}$,n=$\frac{\sqrt{6}}{2}$,可得双曲线的实轴长2a=$\sqrt{(\sqrt{2}+1)^{2}+(\frac{\sqrt{6}}{2})^{2}}$-$\sqrt{(\sqrt{2}-1)^{2}+(\frac{\sqrt{6}}{2})^{2}}$
=$\frac{\sqrt{9+4\sqrt{2}}}{\sqrt{2}}-\frac{\sqrt{9-4\sqrt{2}}}{\sqrt{2}}$=$\frac{2\sqrt{2}+1}{\sqrt{2}}-\frac{2\sqrt{2}-1}{\sqrt{2}}$=$\sqrt{2}$,
双曲线的离心率为:$\frac{2}{\sqrt{2}}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查椭圆以及双曲线的简单性质的应用,考查转化思想以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知函数f(x)满足条件:?x∈R,f(x)+f(-x)=0且f(x+t)-f(x)<0(其中t为正数),则函数f(x)的解析式可以是( )
| A. | y=xsinx+3 | B. | y=x3 | C. | y=-sinx | D. | y=-3x |
2.已知A、B为椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右顶点,点P在E上,在△APB中,tanA=$\frac{1}{3}$,tanB=$\frac{3}{4}$,则E的离心率为( )
| A. | $\sqrt{3}$-1 | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
19.已知等差数列{an}的前n项和为Sn,若S10=55,则a3+a8=( )
| A. | 5 | B. | $\frac{11}{2}$ | C. | 10 | D. | 11 |
6.已知直线y=k(x+1)与不等式组$\left\{\begin{array}{l}{x+y-4≤0}\\{3x-y≥0}\\{x>0,y>0}\end{array}\right.$表示的区域有公共点,则k的取值范围为( )
| A. | [0,+∞) | B. | [0,$\frac{3}{2}$] | C. | (0,$\frac{3}{2}$] | D. | ($\frac{3}{2}$,+∞) |
16.如图所示的程序框图中,输出的S的值是( )
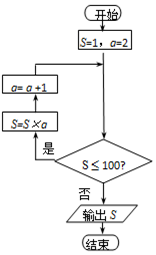

| A. | 80 | B. | 100 | C. | 120 | D. | 140 |
18. 如图,在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子,若撒在图形Ω内和正方形内的豆子数分别为57,100,则图形Ω面积的估计值为( )
如图,在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子,若撒在图形Ω内和正方形内的豆子数分别为57,100,则图形Ω面积的估计值为( )
 如图,在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子,若撒在图形Ω内和正方形内的豆子数分别为57,100,则图形Ω面积的估计值为( )
如图,在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子,若撒在图形Ω内和正方形内的豆子数分别为57,100,则图形Ω面积的估计值为( )| A. | $\frac{57a}{100}$ | B. | $\frac{100a}{57}$ | C. | $\frac{57{a}^{2}}{100}$ | D. | $\frac{100{a}^{2}}{57}$ |