题目内容
16.已知圆x2+y2=16的圆心为P,点Q(a,b)在圆P外,以PQ为直径作圆M与圆P相交于A,B两点.(1)试确定直线QA,QB与圆P的位置关系,若QA=QB=3,写出点Q所在曲线的方程;
(2)若a=4,b=6,求直线AB的方程.
分析 (1)由已知可得∠PAQ=∠PBQ=90°,故直线QA,QB与圆P相切,QA=QB=3,则PQ=5,进而可得点Q所在曲线的方程;
(2)若a=4,b=6,圆M的方程为:(x-2)2+(y-3)2=13,与圆x2+y2=16相减可得公共弦AB所在的直线方程.
解答 解:(1)∵以PQ为直径作圆M与圆P相交于A,B两点.
∴∠PAQ=∠PBQ=90°,
故直线QA,QB与圆P相切,
若QA=QB=3,则PQ=$\sqrt{{3}^{2}+{4}^{2}}$=5,
故Q点在以P(0,0)为圆心,以5为半径的圆上,
即点Q所在曲线的方程为x2+y2=25(7分),
(2)若a=4,b=6,
则PM=$\sqrt{{4}^{2}+{6}^{2}}$=2$\sqrt{13}$,
故圆M的圆心为(2,3),半径为$\sqrt{13}$,
故圆M的方程为:(x-2)2+(y-3)2=13,
与圆x2+y2=16相减可得:4x+6y=16,
故直线AB的方程的方程为:2x+3y-8=0
点评 本题考查的知识点是直线与圆的位置关系,圆的标准方程,两圆相交时的公共弦方程,难度中档.

练习册系列答案
相关题目
8.动点A(x,y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,6秒旋转一周.已知时间t=0时,点A的坐标是($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),则当0≤t≤6时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是( )
| A. | [0,1] | B. | [4,6] | C. | [1,3] | D. | [0,1]和[4,6] |
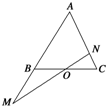 如图所示,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同的两点M,N,若$\overrightarrow{AB}$=m$\overrightarrow{AM}$,$\overrightarrow{AC}$=n$\overrightarrow{AN}$ (m,n>0),则m2+n的范围为[$\frac{7}{4}$,4).
如图所示,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同的两点M,N,若$\overrightarrow{AB}$=m$\overrightarrow{AM}$,$\overrightarrow{AC}$=n$\overrightarrow{AN}$ (m,n>0),则m2+n的范围为[$\frac{7}{4}$,4).