题目内容
6.已知函数f(x)=x3+3x2-5(x∈R)的图象为曲线C.(Ⅰ)当x∈[-2,1]时,求过曲线C上任意一点切线斜率的取值范围;
(Ⅱ)求垂直于直线l:$\left\{\begin{array}{l}{x=\frac{1}{2}+\frac{3\sqrt{10}}{10}t}\\{y=\frac{1}{3}+\frac{\sqrt{10}}{10}t}\end{array}\right.$(t为参数)并且与曲线C相切的直线方程.
分析 (Ⅰ)当x∈[-2,1]时,求导数,求出最值,即可求过曲线C上任意一点切线斜率的取值范围;
(Ⅱ)求出切线斜率,切点坐标,即可得出结论.
解答 解:(Ⅰ)f'(x)=3x2+6x,对称轴x=-1…(2分)
x∈[-2,1]时,f′(x)min=-3,f′(x)max=9…(4分)
∴当x∈[-2,1]时,过曲线C上任意一点切线斜率的取值范围为[-3,9]…(6分)
(Ⅱ)直线l方程可化为:2x-6y+1=0,…(8分)
设切点P(a,b),y'=3x2+6x,切线斜率k=3a2+6a=-3…(10分)
∴a=-1,b=-3,即P(-1,-3),
∴所求切线方程为:3x+y+6=0…(12分)
点评 本题考查导数的几何意义,考查参数方程,考查学生的计算能力,属于中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
17.若定义在R上的可导函数f(x)的导函数为f′(x),在R上满足f′(x)>f(x),且y=f(x-3)为奇函数,f(-6)=-3,则不等式f(x)<3ex的解集为( )
| A. | (0,+∞) | B. | (-3,+∞) | C. | (-∞,0) | D. | (-∞,6) |
1.在极坐标系中,点($\sqrt{2}$,$\frac{π}{4}$)到直线ρsin(θ-$\frac{π}{3}$)=-$\frac{{\sqrt{3}}}{2}$的距离是( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
11.函数f(x)=$\sqrt{3}$x+2cosx,x∈(0,π)上单调减区间为( )
| A. | ($\frac{π}{3}$,$\frac{2π}{3}$) | B. | ($\frac{π}{6}$,$\frac{5π}{6}$) | C. | (0,$\frac{π}{3}$),($\frac{2π}{3}$,π) | D. | (0,$\frac{π}{6}$),($\frac{5π}{6}$,π) |
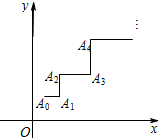 一青蛙从点A0(x0,y0)开始依次水平向右和竖直向上跳动,其落点坐标依次是Ai(xi,yi)(i∈N*),(如图,A0(x0,y0)的坐标以已知条件为准),Sn表示青蛙从点A0到点An所经过的路程.
一青蛙从点A0(x0,y0)开始依次水平向右和竖直向上跳动,其落点坐标依次是Ai(xi,yi)(i∈N*),(如图,A0(x0,y0)的坐标以已知条件为准),Sn表示青蛙从点A0到点An所经过的路程.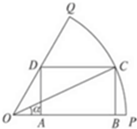 如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的动点,四边形ABCD是扇形的内接矩形,记∠COP=α,矩形的面积为S;
如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的动点,四边形ABCD是扇形的内接矩形,记∠COP=α,矩形的面积为S;