题目内容
已知 为椭圆
为椭圆 ,
, 的左右焦点,
的左右焦点, 是坐标原点,过
是坐标原点,过 作垂直于
作垂直于 轴的直线
轴的直线 交椭圆于
交椭圆于 ,设
,设 .
.
(1)证明: 成等比数列;
成等比数列;
(2)若 的坐标为
的坐标为 ,求椭圆
,求椭圆 的方程;
的方程;
(3)在(2)的椭圆中,过 的直线
的直线 与椭圆
与椭圆 交于
交于 、
、 两点,若
两点,若 ,求直线
,求直线 的方程.
的方程.

(1)∵ 是函数
是函数 的极值点,
的极值点,
∴ ∴
∴
(2) 中
中 对
对
∴ 的两个不相等的实根
的两个不相等的实根
由韦达定理知 ,
,
∴|x1|+|x2|=|x1-x2|=
∴ 即
即
令
 ;
;

 ∴b≤4
∴b≤4
22. (1)证明:由条件知M点的坐标为 ,其中
,其中 ,
,
 ,
,  ,即
,即 成等比数列.
成等比数列.
(2)由条件知 ,
,

 椭圆方程为
椭圆方程为

所以 由
由 得
得


练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
 确定数列
确定数列 ,
, .若函数
.若函数 能确定数列
能确定数列 ,
, ,则称数列
,则称数列 确定数列
确定数列 ;
; 对任意的正整数
对任意的正整数 恒成立,求实数
恒成立,求实数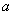 的取值范围;
的取值范围; (
( 为正整数),若数列
为正整数),若数列 的反数列为
的反数列为 ,
, (公共项
(公共项 为正整数),求数列
为正整数),求数列 .
.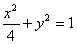 的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、PB与直线l:y=-2分别交于点M、N.
的上、下顶点分别为A、B,点P在椭圆C上且异于点A、B,直线AP、PB与直线l:y=-2分别交于点M、N.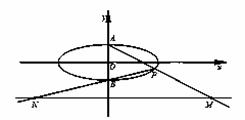
 和圆
和圆 都相切的半径最小的圆的方程是( )
都相切的半径最小的圆的方程是( ) B.
B. 
 D.
D. 
 ,
, ,则函数
,则函数 在
在 上为增函数的概率是 .
上为增函数的概率是 .  ,则
,则
 B.2 C.
B.2 C. D.3
D.3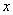 ,符号[
,符号[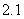 ]=2;[
]=2;[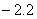 ]=
]=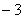 , 这个函数[
, 这个函数[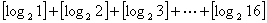 的值为
的值为 B.
B. C.
C. D.
D.

 上定义运算
上定义运算 :
: ,若
,若 对任意实数
对任意实数 都成立,则实数
都成立,则实数 的取值范围是
的取值范围是