题目内容
由函数 确定数列
确定数列 ,
, .若函数
.若函数 能确定数列
能确定数列 ,
, ,则称数列
,则称数列 是数列
是数列 的“反数列”.
的“反数列”.
(1)若函数 确定数列
确定数列 的反数列为
的反数列为 ,求
,求 ;
;
(2)对(1)中的 ,不等式
,不等式 对任意的正整数
对任意的正整数 恒成立,求实数
恒成立,求实数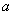 的取值范围;
的取值范围;
(3)设 (
( 为正整数),若数列
为正整数),若数列 的反数列为
的反数列为 ,
, 与
与 的公共项组成的数列为
的公共项组成的数列为 (公共项
(公共项 为正整数),求数列
为正整数),求数列 的前
的前 项和
项和 .
.
解: (1) ,则
,则 ;
;
(2)不等式化为: ,
,
设 ,因为
,因为 ,
,
所以 单调递增,
单调递增,
则 。因此
。因此 ,即
,即 .因为
.因为 ,
,
所以 ,
, 得
得 .
.
(3)当 为奇数时,
为奇数时, ,
, .
.
由 ,则
,则 ,
,
即 ,因此
,因此 ,
,
所以
当 为偶数时,
为偶数时, ,
, .
.
由 得
得 ,即
,即 ,因此
,因此 ,
,
所以 …
…

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 .
. 的最小正周期和对称中心;
的最小正周期和对称中心; 时,求函数
时,求函数 ,
, ,其中
,其中 .
.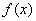 的单调区间(不需要证明);
的单调区间(不需要证明); ,总存在实数
,总存在实数 ,使得不等式
,使得不等式 成立, 求实数
成立, 求实数 的取 值范围.
的取 值范围. ,
, ,则角
,则角 =
=
 的定义域为
的定义域为 ,值域为
,值域为 ,
, 表示的图形可
表示的图形可

 的离心率
的离心率 ,则它的渐近线方程为( )
,则它的渐近线方程为( ) B.
B. C.
C. D.
D.
 =(1,2),
=(1,2), =(-3,2),且(k
=(-3,2),且(k 为椭圆
为椭圆 ,
, 的左右焦点,
的左右焦点, 是坐标原点,过
是坐标原点,过 作垂直于
作垂直于 轴的直线
轴的直线 交椭圆于
交椭圆于 ,设
,设 .
. 成等比数列;
成等比数列; ,求椭圆
,求椭圆 的方程;
的方程;  的直线
的直线 与椭圆
与椭圆 、
、 两点,若
两点,若 ,求直线
,求直线