题目内容
设集合A={x|-2≤x≤4}，B={x|m-3≤x≤m}．
（1）若实数m=5，求A∩B；
（2）若A⊆（∁RB），求实数m的取值范围．
（1）若实数m=5，求A∩B；
（2）若A⊆（∁RB），求实数m的取值范围．
考点：集合的包含关系判断及应用,交、并、补集的混合运算
专题：集合
分析：（1）将m=5代入求出集合B，进而根据集合交集运算定义，可得A∩B
（2）根据A⊆（∁RB），构造关于m的不等式，解不等式求出满足条件的m的取值范围，可得答案．
（2）根据A⊆（∁RB），构造关于m的不等式，解不等式求出满足条件的m的取值范围，可得答案．
解答：
解：（1）当m=5时，B={x|2≤x≤5}．
又∵集合A={x|-2≤x≤4}，
∴{x|2≤x≤4}…（6分）
（2）∵∁RB=B={x|x＜m-3，或x＞m}．
若A⊆（∁RB），则4＜m-3，或-2＞m，
解得：m＜-2，或m＞7，
实数m的取值范围为（-∞，-2）∪（7，+∞）…（12分）
又∵集合A={x|-2≤x≤4}，
∴{x|2≤x≤4}…（6分）
（2）∵∁RB=B={x|x＜m-3，或x＞m}．
若A⊆（∁RB），则4＜m-3，或-2＞m，
解得：m＜-2，或m＞7，
实数m的取值范围为（-∞，-2）∪（7，+∞）…（12分）
点评：本题考查的知识点是集合包含关系判断及应用，交集及其运算，是集合运算与包含关系的综合应用，难度不大．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
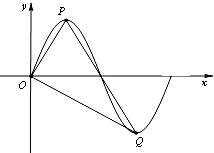某同学用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜
函数f（x）=Asin（ωx+φ），（A，ω，φ是常数，A＞0，ω＞0）的部分图象如图所示，则f（0）=