题目内容
已知函数f(x)=
,若f(2-x2)>f(x),则实数x的取值范围是( )
|
| A、(-∞,-1)∪(2,+∞) |
| B、(-∞,-2)∪(1,+∞) |
| C、(-2,1) |
| D、(-1,2) |
考点:分段函数的应用
专题:函数的性质及应用
分析:根据分段函数的表达式,判断函数的单调性,即可得到结论.
解答:
解:当x≤0时,f(x)=x≤0,且函数单调递增,
当x>0时,f(x)=ln(x+1)>0,且函数单调递增,
故函数在R上为增函数,
则不等式f(2-x2)>f(x),
等价为2-x2>x,
即x2+x-2<0,
解得-2<x<1,
故实数x的取值范围是(-2,1),
故选:C
当x>0时,f(x)=ln(x+1)>0,且函数单调递增,
故函数在R上为增函数,
则不等式f(2-x2)>f(x),
等价为2-x2>x,
即x2+x-2<0,
解得-2<x<1,
故实数x的取值范围是(-2,1),
故选:C
点评:本题主要考查不等式的求解,根据分段函数的表达式,判断函数的单调性是解决本题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
已知集合A={x|x>0},B={x|x≥1},则A∩(∁RB)等于( )
| A、{x|x>1} |
| B、{x|x>0} |
| C、{x|0<x<1} |
| D、{x|x<1} |
已知函数若x,y满足约束条件
,目标函数z=ax+2y仅在点(1,0)处取得最小值,则实数a的取值范围是( )
|
| A、(-4,2) |
| B、(-4,1) |
| C、(-∞,-4)∪(2,+∞) |
| D、(-∞,-4)∪(1,+∞) |
若实数x,y满足
,则
的最小值是( )
|
| y-3 |
| x-2 |
| A、2 | ||
B、
| ||
| C、1 | ||
D、
|
如图是某样本数据的茎叶图,则该样本数据的众数为( )
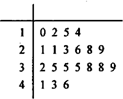

| A、10 | B、21 | C、35 | D、46 |