题目内容
20.已知函数f(x)=$\sqrt{3}sinxcosx+{cos^2}$x,x∈R.(1)求$f(\frac{4π}{3})$;
(2)求函数f(x)的最小正周期与单调减区间.
分析 首项根据二倍角公式和辅助角公式得到:f(x)=sin(2x+$\frac{π}{6}$)+$\frac{1}{2}$.
(1)将$f(\frac{4π}{3})$代入函数解析式,利用特殊角的三角函数值进行解答;
(2)根据正弦函数图象的性质进行解答.
解答 解:$f(x)=\sqrt{3}sinxcosx+{cos^2}x$=$\frac{{\sqrt{3}}}{2}sin2x+\frac{1}{2}cos2x+\frac{1}{2}=sin(2x+\frac{π}{6})+\frac{1}{2}$.
(1)$f(\frac{4π}{3})=sin(\frac{8π}{3}+\frac{π}{6})+\frac{1}{2}=1$;
(2)f(x)的最小正周期为$T=\frac{2π}{2}=π$,
令$\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{3π}{2}+2kπ$,k∈Z,
解得$\frac{π}{6}+kπ≤x≤\frac{2π}{3}+kπ$,
所以函数f(x)的单调减区间为$[{kπ+\frac{π}{6},kπ+\frac{2π}{3}}]$,k∈Z.
点评 本题主要考查三角函数的图象和性质,利用三角函数公式将函数进行化简是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.已知等比数列{an}中,a2a10=6a6,等差数列{bn}中,b4+b6=a6,则数列{bn}的前9项和为( )
| A. | 9 | B. | 27 | C. | 54 | D. | 72 |
5.已知$\overrightarrow a=(-2,4),\overrightarrow b=(x,-2),且\overrightarrow a∥\overrightarrow b,则x的值为$( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
12.设F1、F2是椭圆$\frac{{x}^{2}}{5}+\frac{{y}^{2}}{2}$=1的两个焦点,点P在椭圆上,当△F1PF2的面积为2时,$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}$=( )
| A. | -$\frac{2\sqrt{6}}{3}$ | B. | 0 | C. | 1 | D. | $\frac{\sqrt{3}}{3}$ |
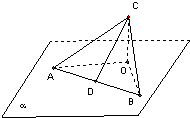 如图:已知三角形ABC,∠ACB=90°,AB在平面α内,C不在平面α内,点C在平面α内的射影为O,CA,CB与平面α所成角分别为30°,45°,CD⊥AB,D为垂足,则CD与平面α所成角60°.
如图:已知三角形ABC,∠ACB=90°,AB在平面α内,C不在平面α内,点C在平面α内的射影为O,CA,CB与平面α所成角分别为30°,45°,CD⊥AB,D为垂足,则CD与平面α所成角60°.