题目内容
4．不等式|x-3|-|x+1|≤a2-3a对任意实数x恒成立，则实数a的取值范围是（ ）| A． | （-∞，1]∪[4，+∞） | B． | [-1，4] | C． | [-4，1] | D． | （-∞，-4]∪[1，+∞） |
分析 先去绝对值符号确定|x+3|-|x-1|的取值范围，然后让a2-3a大于它的最大值，求解即可．
解答 解：令y=|x+3|-|x-1|
当x＞1时，y=x+3-x+1=4
当x＜-3时，y=-x-3+x-1=-4
当-3≤x≤1时，y=x+3+x-1=2x+2 所以-4≤y≤4
所以要使得不等式|x+3|-|x-1|≤a2-3a对任意实数x恒成立
只要a2-3a≥4即可，
∴a≤-1或a≥4，
故选：A．
点评 本题主要考查不等式恒成立问题．大于一个函数式只需要大于它的最大值即可．
练习册系列答案
相关题目
14．函数y=cos（$\frac{1}{3}$x-φ），（0≤φ≤π）是R上的奇函数，则φ的值是（ ）
| A． | 0 | B． | $\frac{π}{4}$ | C． | $\frac{π}{2}$ | D． | π |
12．从4款甲型和5款乙型智能手机中任取3款，其中至少要甲乙型号各一款，则不同的取法共有（ ）
| A． | 140种 | B． | 80种 | C． | 70种 | D． | 35种 |
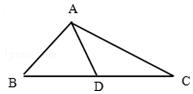如图，在△ABC中，BC边上的中线AD长为3，且BD=2，sinB=$\frac{3\sqrt{6}}{8}$．