题目内容
在等比数列{an}中，若a4a6a8a10a12=243，则
的值为 ．
| a102 |
| a12 |
考点：等比数列的性质
专题：计算题,等差数列与等比数列
分析：根据等比数列的性质可得a4a12=a6a10=a82，化简已知的等式，求出a8的值，再根据等比数列的性质得a8•a12=a102，变形可得所求式子的值．
解答：
解：∵a4a6a8a10a12=a85=243，
∴a8=3，又a8•a12=a102，
则
=a8=3．
故答案为：3
∴a8=3，又a8•a12=a102，
则
| a102 |
| a12 |
故答案为：3
点评：此题考查了等比数列性质的运用，是高考中常考的基本题型．熟练掌握等比数列的性质是解本题的关键．
练习册系列答案
相关题目
关于函数f（x）=ax（0＜a＜1），下列说法正确的是（ ）
| A、定义域为R+ |
| B、值域为R+ |
| C、图象关于x轴对称 |
| D、为增函数 |
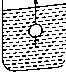如图所示，在一个盛满水的圆柱形容器内的水面下有一个用细绳吊着的薄壁小球，小球下方有一个小孔，当慢慢地、均匀地将小球从水下面往上拉动时，圆柱形容器内水面的高度h与时间t的函数关系图象大致为（ ）A、 |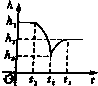
B、 |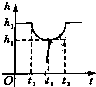
C、 |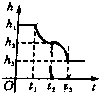
D、 |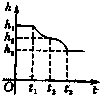
如果f（x）的定义域为R，f（x+2）=f（x+1）-f（x），且f（1）=lg3-lg2，f（2）=lg3+lg5，则f（2008）=（ ）
| A、1 | B、-1 |
| C、lg2-lg3 | D、-lg3-lg5 |
已知向量
，
不共线，若
=λ1
+
，
=
+λ2
，则“A、B、C三点共线”是“λ1λ2=1”的（ ）
| a |
| b |
| AB |
| a |
| b |
| AC |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
给定条件p：|x+1|＞2，条件q：
＞1，则?q是?p的（ ）
| 1 |
| 3-x |
| A、充要条件 |
| B、必要而不充分条件 |
| C、充分而不必要条件 |
| D、既不充分也不必要条件 |
直线l：2x+y+5=0上的点与原点的距离的最小值是（ ）
| A、2 | ||
B、
| ||
C、
| ||
D、2
|