题目内容
若sinα>tanα>cotα(-
<α<
),则α∈( )
| π |
| 2 |
| π |
| 2 |
A.(-
| B.(-
| C.(0,
| D.(
|
∵sinα>
,-
<α<
∴cosαsinα-sinα>0,即sinα(cosα-1)>0
∵cosα-1<0
∴sinα<0,-
<α<0
∵tanα>cota
∴
>
∵-
<α<0
∴
>-1
即tanα>-1
∴α>-
综合得-
<α<0
故选B
| sinα |
| cosα |
| π |
| 2 |
| π |
| 2 |
∴cosαsinα-sinα>0,即sinα(cosα-1)>0
∵cosα-1<0
∴sinα<0,-
| π |
| 2 |
∵tanα>cota
∴
| sinα |
| cosα |
| cosα |
| sinα |
∵-
| π |
| 2 |
∴
| sinα |
| cosα |
即tanα>-1
∴α>-
| π |
| 4 |
综合得-
| π |
| 4 |
故选B

练习册系列答案
相关题目
若sinα+cosα=tanα(0<α<
),则α所在的区间( )
| π |
| 2 |
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
若sinα>tanα>cotα(-
<α<
),则α∈( )
| π |
| 2 |
| π |
| 2 |
A、(-
| ||||
B、(-
| ||||
C、(0,
| ||||
D、(
|
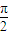 ),则α所在的区间( )
),则α所在的区间( )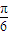 )
)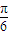 ,
,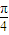 )
)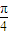 ,
,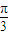 )
) ,
,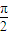 )
)