Question

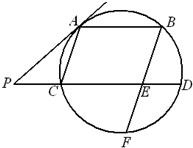如图，AB、CD是圆的两条平行弦，BE∥AC，BE交CD于E、交圆于F，过A点的切线交DC的延长线于P，PC=ED=1，PA=2．
（Ⅰ）求AC的长；
（Ⅱ）求证：BE=EF．

Answer 1

分析：（1）由PA是圆的切线结合切割线定理得比例关系，求得PD，再由角相等得三角形相似：△PAC∽△CBA，从而求得AC的长；
（2）欲求证：“BE=EF”，可先分别求出它们的值，比较即可，求解时可结合圆中相交弦的乘积关系．

解答：解：（I）∵PA²=PC•PD，PA=2，PC=1，
∴PD=4，
又∵PC=ED=1，∴CE=2，
∵∠PAC=∠CBA，∠PCA=∠CAB，
∴△PAC∽△CBA，∴

PC

AC

=

AC

AB

，
∴AC²=PC•AB=2，∴AC=

2

（5分）
（II）∵BE=AC=

2

，CE=2，而CE•ED=BE•EF，
∴EF=

2•1

2

=

2

，∴EF=BE．（10分）

点评：本题主要考查与圆有关的比例线段、圆中的切割线定理以及相似三角形的知识，属于基础题．