题目内容
 (2013•和平区二模)如图,AB、CD是圆O的两条平行弦,AF∥BD交CD于点E,交圆为O于点F,过B点的切线交CD的延长线于点P,若PD=CE=1,PB=
(2013•和平区二模)如图,AB、CD是圆O的两条平行弦,AF∥BD交CD于点E,交圆为O于点F,过B点的切线交CD的延长线于点P,若PD=CE=1,PB=| 5 |
| 3 |
| 3 |
分析:根据切割线定理PB2=PD×PC,算出CD=4,得PC=5,ED=CD-CE=3.由△BPD∽△CPB得
=
=
,设BD=x得CB=
x.设AF、BC的交点为G,利用平等线分线段成比例结合平行四边形的性质,算出GE=
x、CG=
x、BG=
x且AG=
x.然后利用相交弦定理AG•GF=CG•BG,算出GF=
x,从而EF=GF-GE=x.最后根据AE•EF=CE•ED,即可算出BD的长.
| BD |
| CB |
| PB |
| CP |
| ||
| 5 |
| 5 |
| 1 |
| 4 |
| ||
| 4 |
3
| ||
| 4 |
| 3 |
| 4 |
| 5 |
| 4 |
解答: 解:∵直线PB切圆O于点B,PDC是圆O的割线
解:∵直线PB切圆O于点B,PDC是圆O的割线
∴PB2=PD×PC,得(
)2=1×(1+CD),
解得CD=4,得PC=5,ED=CD-CE=3
∵∠PBD=∠PCB,∠BPD=∠CPB
∴△BPD∽△CPB,可得
=
=
设BD=x,则CB=
x,设AF、BC的交点为G
∵AE∥BD,得
=
=
,
∴GE=
BD=
x;CG=
CB=
x,BG=
x,
平等四边形ABDE中,AE=BD=x,得AG=AE-GE=
x
由相交弦定理,得AG•GF=CG•BG,即
x•GF=
x•
x
解得GF=
x,可得EF=GF-GE=
x-
x=x
又∵AE•EF=CE•ED,AE=EF=x,CE=1且ED=3
∴x2=1×3=3,解之得x=
,即BD的长为
故答案为:
 解:∵直线PB切圆O于点B,PDC是圆O的割线
解:∵直线PB切圆O于点B,PDC是圆O的割线∴PB2=PD×PC,得(
| 5 |
解得CD=4,得PC=5,ED=CD-CE=3
∵∠PBD=∠PCB,∠BPD=∠CPB
∴△BPD∽△CPB,可得
| BD |
| CB |
| PB |
| CP |
| ||
| 5 |
设BD=x,则CB=
| 5 |
∵AE∥BD,得
| GE |
| BD |
| CE |
| CD |
| 1 |
| 4 |
∴GE=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| ||
| 4 |
3
| ||
| 4 |
平等四边形ABDE中,AE=BD=x,得AG=AE-GE=
| 3 |
| 4 |
由相交弦定理,得AG•GF=CG•BG,即
| 3 |
| 4 |
| ||
| 4 |
3
| ||
| 4 |
解得GF=
| 5 |
| 4 |
| 5 |
| 4 |
| 1 |
| 4 |
又∵AE•EF=CE•ED,AE=EF=x,CE=1且ED=3
∴x2=1×3=3,解之得x=
| 3 |
| 3 |
故答案为:
| 3 |
点评:本题给出圆内的平行线和圆的切线,在已知切线PB长的情况下求线段BD的长.着重考查了圆当中的比例线段、平行线的性质、相似三角形的判定与性质等知识,属于中档题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
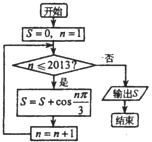 (2013•和平区二模)阅读如图所示的程序框图,运行相应的程序,则输出的结果S的值为( )
(2013•和平区二模)阅读如图所示的程序框图,运行相应的程序,则输出的结果S的值为( ) (2013•和平区二模)已知函数y=Asin(ωx+φ)(A>0,ω>0),|φ|<π)的部分图象如图所示,则它的解析式为( )
(2013•和平区二模)已知函数y=Asin(ωx+φ)(A>0,ω>0),|φ|<π)的部分图象如图所示,则它的解析式为( )