题目内容
 (选做)如图,AB,CD是圆O的两条线,且AB是线段CD的中垂线,已知AB=6,CD=2
(选做)如图,AB,CD是圆O的两条线,且AB是线段CD的中垂线,已知AB=6,CD=2| 5 |
| 6 |
| 6 |
分析:连接BC,设AB,CD相交于点E,AE=x,由AB是线段CD的垂直平分线,知AB是圆的直径,∠ACB=90°,推出EB=6-x,CE=
.由射影定理求出x,然后求解BC的长度.
| 5 |
解答: 解:连接BC,设AB,CD相交于点E,AE=x,
解:连接BC,设AB,CD相交于点E,AE=x,
∵AB是线段CD的垂直平分线,
∴AB是圆的直径,∠ACB=90°,
则EB=6-x,CE=
.由射影定理得CE2=AE•EB,
即有x(6-x)=5,解得x=1(舍)或x=5,
∴BC2=BE•AB=1×6=6,即BC=
.
故答案为:
.
 解:连接BC,设AB,CD相交于点E,AE=x,
解:连接BC,设AB,CD相交于点E,AE=x,∵AB是线段CD的垂直平分线,
∴AB是圆的直径,∠ACB=90°,
则EB=6-x,CE=
| 5 |
即有x(6-x)=5,解得x=1(舍)或x=5,
∴BC2=BE•AB=1×6=6,即BC=
| 6 |
故答案为:
| 6 |
点评:本题考查线段长度的求法,是基础题,解题时要认真审题,注意圆的性质、射影定理的灵活运用.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
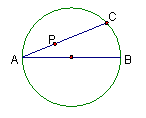 动点P的轨迹方程为 .
动点P的轨迹方程为 .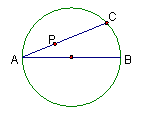 动点P的轨迹方程为 .
动点P的轨迹方程为 .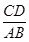 等于
.
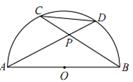
等于
.
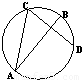 (选做)如图,AB,CD是圆O的两条线,且AB是线段CD的中垂线,已知
(选做)如图,AB,CD是圆O的两条线,且AB是线段CD的中垂线,已知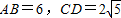 ,则线段BC的长度为 .
,则线段BC的长度为 .