题目内容
如图所示,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC=90°,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点.求AB与平面BDF所成角的正弦值.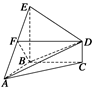

AB与平面BDF所成角的正弦值为 .
.
 .
.以点B为原点,BA、BC、BE所在的直线分别为x,y,z轴,建立如图所示的空间直角坐标系,则

B(0,0,0),A(2,0,0),C(0,2,0),D(0,2,1),E(0,0,2),F(1,0,1).
∴ =(0,2,1),
=(0,2,1), =(1,-2,0).
=(1,-2,0).
设平面BDF的一个法向量为
n=(2,a,b),
∵n⊥ ,n⊥
,n⊥ ,
,
∴
即
解得a=1,b=-2.∴n=(2,1,-2).
设AB与平面BDF所成的角为 ,则法向量n与
,则法向量n与 的夹角为
的夹角为 -
- ,
,
∴cos( -
- )=
)= =
= =
= ,
,
即sin =
= ,故AB与平面BDF所成角的正弦值为
,故AB与平面BDF所成角的正弦值为 .
.

B(0,0,0),A(2,0,0),C(0,2,0),D(0,2,1),E(0,0,2),F(1,0,1).
∴
 =(0,2,1),
=(0,2,1), =(1,-2,0).
=(1,-2,0).设平面BDF的一个法向量为
n=(2,a,b),
∵n⊥
 ,n⊥
,n⊥ ,
,∴

即

解得a=1,b=-2.∴n=(2,1,-2).
设AB与平面BDF所成的角为
 ,则法向量n与
,则法向量n与 的夹角为
的夹角为 -
- ,
,∴cos(
 -
- )=
)= =
= =
= ,
,即sin
 =
= ,故AB与平面BDF所成角的正弦值为
,故AB与平面BDF所成角的正弦值为 .
.
练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
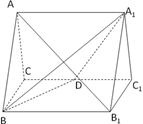
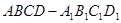 中,底面边长为
中,底面边长为 ,侧棱长为4,E,F分别为棱AB,CD的中点,
,侧棱长为4,E,F分别为棱AB,CD的中点, .则三棱锥
.则三棱锥 的体积V( )
的体积V( )
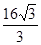


 的正方体
的正方体 中,则平面
中,则平面 与平面
与平面 间的距离 ( )
间的距离 ( )



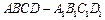 的棱长为2,
的棱长为2,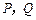 分别是
分别是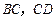 上的动点,且
上的动点,且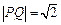 ,确定
,确定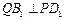 .
. A1N=
A1N= NB1,P为底面正方形A1B1C1D1的中心.求证:MN⊥MC,MP⊥B1C.
NB1,P为底面正方形A1B1C1D1的中心.求证:MN⊥MC,MP⊥B1C. 是三条不同的直线,
是三条不同的直线,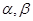 是两个不同的平面,下列命题为真命题的是( )
是两个不同的平面,下列命题为真命题的是( )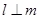 ,
,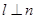 ,
,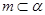 ,
,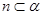 ,则
,则
 ∥
∥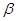 ,
,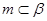 ,则
,则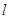 ∥
∥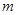 ,
,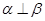 ,
,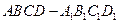 的棱长是
的棱长是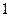 ,则直线
,则直线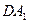 与
与 间的距离为 。
间的距离为 。