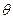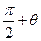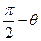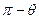题目内容
正四棱柱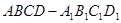 中,底面边长为
中,底面边长为 ,侧棱长为4,E,F分别为棱AB,CD的中点,
,侧棱长为4,E,F分别为棱AB,CD的中点, .则三棱锥
.则三棱锥 的体积V( )
的体积V( )
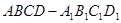 中,底面边长为
中,底面边长为 ,侧棱长为4,E,F分别为棱AB,CD的中点,
,侧棱长为4,E,F分别为棱AB,CD的中点, .则三棱锥
.则三棱锥 的体积V( )
的体积V( )A. | B.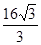 | C. | D. |
C
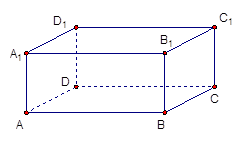
试题分析:如图,
 ,求得
,求得 ,
, ,则三棱锥
,则三棱锥 的体积
的体积 。故选C。
。故选C。
点评:求空间几何体的体积和表面积是重要的考点。在求三棱锥的体积时,四个面都可以作为底面,我们需要灵活应用。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中,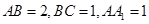
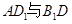 所成角;
所成角;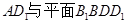 所成角的正弦.
所成角的正弦.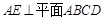 ,
, ,
,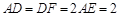 .
.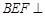 平面
平面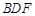 ;
;
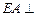 平面
平面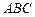 ,
,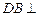 平面
平面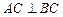 ,
,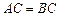
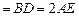 ,
,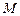 是
是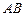 的中点.建立适当的空间直角坐标系,解决下列问题:
的中点.建立适当的空间直角坐标系,解决下列问题: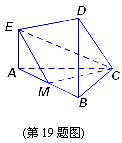
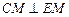 ;
;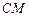 与平面
与平面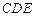 所成角的大小.
所成角的大小.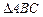 是边长为2的等边三角形,
是边长为2的等边三角形,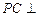 平面
平面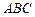 ,
,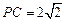 ,
,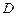 是
是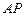 上一动点.
上一动点.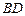 与平面
与平面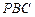 所成的角的正弦值;
所成的角的正弦值;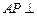 平面
平面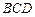 ?请说明理
?请说明理 由.
由.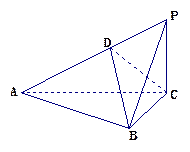
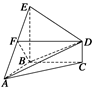
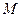 是PC的中点,设
是PC的中点,设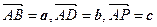 .
.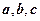 表示出向量
表示出向量 ;
;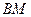 的长.
的长.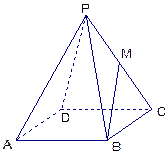
 中,若
中,若 则
则 ( )
( )


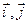 分别是
分别是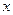 轴,
轴,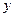 轴正方向上的单位向量,
轴正方向上的单位向量,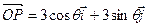 ,
,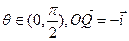 。若用?来表示
。若用?来表示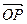 与
与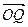 的夹角,则?等于 ( )
的夹角,则?等于 ( )