题目内容
5.36的所有正约数之和可按如下方法得到:因为36=22×32,所以36的所有正约数之和为(1+3+32)+(2+2×3+2×32)+(22+22×3+22×32)=(1+2+22)(1+3+32)=91,参照上述方法,可得100的所有正约数之和为( )| A. | 217 | B. | 273 | C. | 455 | D. | 651 |
分析 根据题意,类比36的所有正约数之和的方法,分析100的所有正约数之和为(1+2+22)(1+5+52),计算可得答案.
解答 解:根据题意,由36的所有正约数之和的方法:
100的所有正约数之和可按如下方法得到:因为100=22×52,
所以100的所有正约数之和为(1+2+22)(1+5+52)=217.
可求得100的所有正约数之和为217;
故选:A.
点评 本题考查简单的合情推理应用,关键是认真分析36的所有正约数之和的求法,并应用到100的正约数之和的计算.

练习册系列答案
相关题目
16.如图,在△ABC中,$\overrightarrow{AN}=\frac{1}{4}\overrightarrow{NC}$,P是BN上的一点,若$\overrightarrow{AP}=m\overrightarrow{AB}+\frac{2}{11}\overrightarrow{AC}$,则实数m的值为( )
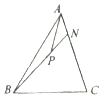

| A. | $\frac{9}{11}$ | B. | $\frac{2}{11}$ | C. | $\frac{3}{11}$ | D. | $\frac{1}{11}$ |
20.已知一组数据3、4、5、s、t的平均数是4,中位数是m,对于任意实数s、t,从3、4、5、s、t、m这组数据中任取一个,取到数字4的概率的最大值为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
15.过点P(4,3),且斜率为$\frac{2}{3}$的直线的参数方程为( )
| A. | $\left\{\begin{array}{l}{x=4+\frac{3}{\sqrt{13}}t}\\{y=3+\frac{2}{\sqrt{13}}t}\end{array}\right.$(t为参数) | B. | $\left\{\begin{array}{l}{x=3+\frac{3}{\sqrt{13}}t}\\{y=4+\frac{2}{\sqrt{13}}t}\end{array}\right.$(t为参数) | ||
| C. | $\left\{\begin{array}{l}{x=4+\frac{2}{\sqrt{13}}t}\\{y=3+\frac{3}{\sqrt{13}}t}\end{array}\right.$(t为参数) | D. | $\left\{\begin{array}{l}{x=3+\frac{2}{\sqrt{13}}t}\\{y=4+\frac{3}{\sqrt{13}}t}\end{array}\right.$(t为参数) |
