题目内容
14.设D为△ABC所在平面内一点,$\overrightarrow{BC}=5\overrightarrow{CD}$,若$\overrightarrow{AB}=x\overrightarrow{AC}+y\overrightarrow{AD}$,则x+2y=-4.分析 由已知得$\overrightarrow{AC}-\overrightarrow{AB}=5({\overrightarrow{AD}-\overrightarrow{AC}})$,从而$\overrightarrow{AB}=6\overrightarrow{AC}-5\overrightarrow{AD}$,由此能求出x+2y的值.
解答 解:∵$\overrightarrow{BC}=5\overrightarrow{CD}$,
∴$\overrightarrow{AC}-\overrightarrow{AB}=5({\overrightarrow{AD}-\overrightarrow{AC}})$,
即$\overrightarrow{AB}=6\overrightarrow{AC}-5\overrightarrow{AD}$,
∴x=6,y=-5,∴x+2y=-4.
故答案为:-4.
点评 本题考查代数式求和,是基础题,解题时要认真审题,注意平面向量运算法则的合理运用.

练习册系列答案
相关题目
5.给出下列四个命题:
①已知m,n是常数,“mn<0”是“mx2+ny2=1表示双曲线的充分不必要条件”;
②命题p:“?x∈R,sinx≤1”的否定是¬p:“?x0∈R,sinx0>1”;
③已知命题p和q,若p∨q是假命题,则p与q中必一真一假;
④命题“若a>b>0,则a2>b2”的逆命题是假命题.
其中真命题的序号是( )
①已知m,n是常数,“mn<0”是“mx2+ny2=1表示双曲线的充分不必要条件”;
②命题p:“?x∈R,sinx≤1”的否定是¬p:“?x0∈R,sinx0>1”;
③已知命题p和q,若p∨q是假命题,则p与q中必一真一假;
④命题“若a>b>0,则a2>b2”的逆命题是假命题.
其中真命题的序号是( )
| A. | ①②④ | B. | ①③④ | C. | ②④ | D. | ②③ |
2.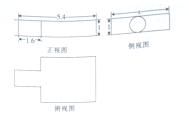 中国古代数学名著《九章算术》中记载了公元前344年商鞅制造一种标准量器-商鞅铜方升,其三视图(单位:寸)如图所示,若π取3,其体积为12.6(立方寸),则图中x的为( )
中国古代数学名著《九章算术》中记载了公元前344年商鞅制造一种标准量器-商鞅铜方升,其三视图(单位:寸)如图所示,若π取3,其体积为12.6(立方寸),则图中x的为( )
 中国古代数学名著《九章算术》中记载了公元前344年商鞅制造一种标准量器-商鞅铜方升,其三视图(单位:寸)如图所示,若π取3,其体积为12.6(立方寸),则图中x的为( )
中国古代数学名著《九章算术》中记载了公元前344年商鞅制造一种标准量器-商鞅铜方升,其三视图(单位:寸)如图所示,若π取3,其体积为12.6(立方寸),则图中x的为( )| A. | 2.5 | B. | 3 | C. | 3.2 | D. | 4 |
9.在等差数列{an}中,已知a3+a8=6,则3a2+a16的值为( )
| A. | 24 | B. | 18 | C. | 16 | D. | 12 |
6.函数$f(x)=-x+\frac{1}{x}$在$[{-2,-\frac{1}{3}}]$上的最大值是( )
| A. | $\frac{3}{2}$ | B. | $-\frac{8}{3}$ | C. | -2 | D. | 2 |
3.抽样统计甲、乙两名学生的5次训练成绩(单位:分),结果如下:
则成绩较为稳定(方差较小)的那位学生成绩的方差为20.
| 学生 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次 |
| 甲 | 65 | 80 | 70 | 85 | 75 |
| 乙 | 80 | 70 | 75 | 80 | 70 |