题目内容

等差数列{an}的公差为d，则数列{3an}是（　　）
A、非等差数列
B、公差为d的等差数列
C、公差为
1
3
d的等差数列
D、公差为3d的等差数列
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：利用等差数列的定义，可得结论．
解答： 解：∵等差数列{an}的公差为d，
∴an-an-1=d，
∴3an-3an-1=3d，
∴数列{3an}是公差为3d的等差数列．
故选：D．
点评：本题考查了等差数列的通项公式，比较基础．
练习册系列答案
相关题目
已知A={（x，y）|y=-x+3}，B={（x，y）|y=2x-1}，求A∩B．
已知函数f（x）满足f（4）=5，且f（x）在R上的导数满足f′（x）-1＜0，则不等式f（x2）＜x2+1的解集为（　　）
A、（-∞，-2）∪（2，+∞）
B、（2，+∞）
C、（2，+∞）
D、以上都不对
已知函数f（x）=sinx+cosx，则函数f（x）的一个单调递增区间为（　　）
A、(0，
π
4
)
B、(
π
4
，
π
2
)
C、(
π
2
，
3π
4
)
D、(
3π
4
，π)
（A题）下列求导运算正确的是（　　）
A、（x+
3
x
）′=1+
3
x2
B、（3x）′=3xlog3e
C、（log2x）′=
1
xln2
D、（x2cos x）′=-2xsin x
对于实数a和b，定义运算“*”：
a2-ab，a≤b
b2-ab，a＞b
，设f（x）=（2x-1）*（x-1），且关于x的方程f（x）=a（a∈R）恰有三个互不相等的实数根，则实数a的取值范围
是（　　）
A、（0，
1
4
）
B、[0，
1
4
]
C、[0，
1
16
]
D、（0，
1
4
]∪（1，+∞）
已知某一随机变量ξ的概率分布列如下，则b的值为（　　）
ξ4a9
p0.50.1b
A、0.6B、0.5
C、0.4D、0.1
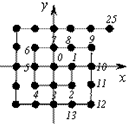如图，将平面直角坐标系中的格点（横、纵坐标均为整 数的点）按如  下规则标上数字标签：原点（0，0）处标0，点（1，0）处标1，点（1，-1）处标2，点（0，-1）处标3，点（-1，-1）处标4，点（-1，0）处标5，…，依此类推，则标签2012×2013对应的格点的坐标 为（　　）
A、（-1006，1006）
B、（1005，-1006）
C、（1005，1006）
D、（1006，1006）
下列周期为
π
2
的函数为（　　）
A、y=sin（2x+
π
6
）
B、y=2tan（x+
π
7
）
C、y=cos3x
D、y=tan2x

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网