题目内容
4.(I)已知向量$\overrightarrow{OA}=(1,-2)$,$\overrightarrow{OB}=(4,-1)$,$\overrightarrow{OC}=({m,m+1})$.若$\overrightarrow{AB}∥\overrightarrow{OC}$,求实数m的值;( II)已知矩形ABCD的边长为1,点E是边AB的中点,求$\overrightarrow{DE}•\overrightarrow{CB}$的值.
分析 (Ⅰ)由已知向量的坐标求得$\overrightarrow{AB}$的坐标,再由向量共线的坐标运算得答案;
(Ⅱ)由题意建系,利用坐标求解.
解答 解:(Ⅰ)∵$\overrightarrow{OA}=(1,-2)$,$\overrightarrow{OB}=(4,-1)$,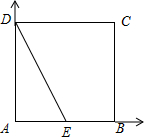
∴$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=(3,1)$,
又$\overrightarrow{OC}=({m,m+1})$,且$\overrightarrow{AB}∥\overrightarrow{OC}$,
∴3(m+1)-m=0,得m=-$\frac{3}{2}$;
(Ⅱ)如图,D(0,1),E($\frac{1}{2}$,0),B(1,0),C(1,1),
则$\overrightarrow{DE}=(\frac{1}{2},-1)$,$\overrightarrow{CB}=(0,-1)$,
∴$\overrightarrow{DE}•\overrightarrow{CB}$=$\frac{1}{2}×0+(-1)×(-1)=1$.
点评 本题考查平面向量的数量积运算,建系求解起到事半功倍的效果,是中档题.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均不低于40分)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图.
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均不低于40分)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图. 如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,点P(3,1)在椭圆上,△PF1F2的面积为2$\sqrt{2}$,点Q是PF2的延长线与椭圆的交点.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,点P(3,1)在椭圆上,△PF1F2的面积为2$\sqrt{2}$,点Q是PF2的延长线与椭圆的交点.