题目内容
11.已知函数y=f(1-x)的图象如图所示,则y=f(1+x)的图象为( )
| A. |  | B. |  | C. |  | D. |  |
分析 带入特殊点即可选出答案.
解答 解:因为y=f(1-x)的图象过点(1,a),
所以f(0)=a,
所以y=f(1+x)的图象过点(-1,a).
故选B.
点评 本题考查了函数图象变换,是基础题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
16.已知f(x)=1+1ogx2+1og${\;}_{{x}^{2}}$4+1og${\;}_{{x}^{3}}$8,则使f(x)<0的x的取值范围是( )
| A. | (0,1) | B. | (1,+∞) | C. | ($\frac{1}{8}$,1) | D. | (0,$\frac{1}{8}$) |
3.复数$z=\frac{1-3i}{1+i}$的模是( )
| A. | 2 | B. | 1 | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
20. 如图中的曲线是指数函数的图象,已知a的值分别取$\sqrt{2}$,$\frac{4}{3}$,$\frac{3}{10}$,$\frac{1}{5}$,则相应于曲线C1,C2,C3,C4的a依次为( )
如图中的曲线是指数函数的图象,已知a的值分别取$\sqrt{2}$,$\frac{4}{3}$,$\frac{3}{10}$,$\frac{1}{5}$,则相应于曲线C1,C2,C3,C4的a依次为( )
 如图中的曲线是指数函数的图象,已知a的值分别取$\sqrt{2}$,$\frac{4}{3}$,$\frac{3}{10}$,$\frac{1}{5}$,则相应于曲线C1,C2,C3,C4的a依次为( )
如图中的曲线是指数函数的图象,已知a的值分别取$\sqrt{2}$,$\frac{4}{3}$,$\frac{3}{10}$,$\frac{1}{5}$,则相应于曲线C1,C2,C3,C4的a依次为( )| A. | $\frac{4}{3}$,$\sqrt{2}$,$\frac{1}{5}$,$\frac{3}{10}$ | B. | $\sqrt{2}$,$\frac{4}{3}$,$\frac{3}{10}$,$\frac{1}{5}$ | C. | $\frac{3}{10}$,$\frac{1}{5}$,$\sqrt{2}$,$\frac{4}{3}$ | D. | $\frac{1}{5}$,$\frac{3}{10}$,$\frac{4}{3}$,$\sqrt{2}$ |
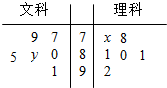 某中学从文、理科实验班中各选6名同学去参加复旦大学自主招生考试,其数学成绩茎叶图如图,其中文科生的成绩的众数为85,理科生成绩平均数为81,则x•y的值为( )
某中学从文、理科实验班中各选6名同学去参加复旦大学自主招生考试,其数学成绩茎叶图如图,其中文科生的成绩的众数为85,理科生成绩平均数为81,则x•y的值为( )