题目内容
已知g(x)=-x2-3,f(x)是二次函数,当x∈[-1,2]时,f(x)的最小值是1,且f(x)+g(x)是奇函数,求f(x)的表达式.
解析:设f(x)=ax2+bx+c(a≠0),
则f(x)+g(x)=(a-1)x2+bx+c-3是奇函数,
∴
∴f(x)=x2+bx+3= 2+3-
2+3- b2.
b2.
(1)当-1≤- ≤2即-4≤b≤2时,
≤2即-4≤b≤2时,
最小值为3- b2=1⇒b=±2
b2=1⇒b=±2 ,
,
∴b=-2 .∴f(x)=x2-2
.∴f(x)=x2-2 x+3.
x+3.
(2)当- >2,即b<-4时,f(2)=1,无解.
>2,即b<-4时,f(2)=1,无解.
(3)当- <-1,即b>2时,f(-1)=1⇒b=3,
<-1,即b>2时,f(-1)=1⇒b=3,
∴f(x)=x2+3x+3.
综上所述,f(x)=x2-2 x+3或f(x)=x2+3x+3.
x+3或f(x)=x2+3x+3.

练习册系列答案
相关题目
 +ax2+(a-3)x的导函数是偶函数,则曲线y=f(x)在原点处的切线方程为________.
+ax2+(a-3)x的导函数是偶函数,则曲线y=f(x)在原点处的切线方程为________.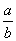 B.
B.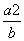 C.
C.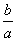 D.
D.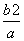

 m](m>0)的最大值为-3,最小值为-4,则实数m的取值范围是( )
m](m>0)的最大值为-3,最小值为-4,则实数m的取值范围是( ) x的图象之间的关系是( )
x的图象之间的关系是( ) (a>1),
(a>1), 函数.
函数.
 B.
B.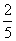 C.
C. D.
D.