题目内容
f(x)是定义在R上的奇函数,当x≥0时f(x)=3x+m(m为常数),则f(-log35)的值为 .
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:本题先通过函数的奇偶性,求出参数m的值,再将自变量转化为正数,结合条件当x≥0时f(x)=3x+m(m为常数),从而求出f(-log35)的值,得到本题结论.
解答:
解:∵f(x)是定义在R上的奇函数,
∴f(-x)=-f(x),f(0)=0,
∵当x≥0时f(x)=3x+m(m为常数),
∴m=-1.
∵当x≥0时f(x)=3x-1,
∵log35>0,
∴f(-log35)=-f(log35)=-(3log35-1)=-4.
故答案为:-4.
∴f(-x)=-f(x),f(0)=0,
∵当x≥0时f(x)=3x+m(m为常数),
∴m=-1.
∵当x≥0时f(x)=3x-1,
∵log35>0,
∴f(-log35)=-f(log35)=-(3log35-1)=-4.
故答案为:-4.
点评:本题考查了函数的奇偶性,本题难度不大,属于基础题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
已知变量x,y满足约束条件
,则z=x+2y的最小值为( )
|
| A、3 | B、1 | C、-5 | D、-6 |
函数y=
的定义域是( )
| 4-3x-x2 |
| A、[-1,4] |
| B、(-∞,-4]∪[1,+∞) |
| C、[-4,1] |
| D、(-∞,-1]∪[4,+∞) |
sin660°等于( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
 已知函数f(x)=|x-1|-x.
已知函数f(x)=|x-1|-x.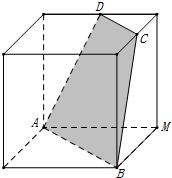 如图,正方体的棱长是a,C,D分别是两条棱的中点.
如图,正方体的棱长是a,C,D分别是两条棱的中点.