题目内容
已知数列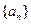 的首项
的首项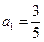 ,
,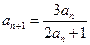 ,
,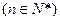 .
.
(1)求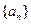 的通项公式;
的通项公式;
(2)证明:对任意的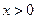 ,
,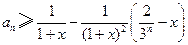 ,
,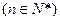 ;
;
(3)证明: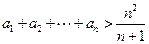 .
.
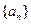 的首项
的首项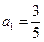 ,
,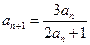 ,
,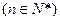 .
.(1)求
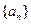 的通项公式;
的通项公式;(2)证明:对任意的
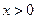 ,
,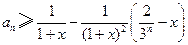 ,
,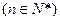 ;
;(3)证明:
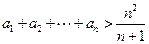 .
.(1)解: ,
, ,
, ,
,
又 ,
, 是以
是以 为首项,
为首项, 为公比的等比数列.
为公比的等比数列.

 ,
, .
.
(2)证法一:由(1)知 ,
,





 ,
, 原不等式成立.
原不等式成立.
证法二:设 ,
,
则
 ,
, 当
当 时,
时, ;当
;当 时,
时, ,
,
 当
当 时,
时, 取得最大值
取得最大值 .
.
 原不等式成立.
原不等式成立.
(3)证明:由(2)知,对任意的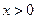 ,有
,有


 .
.
 取
取 ,
,
则 .
.
 原不等式成立.
原不等式成立.
 ,
, ,
, ,
,又
 ,
, 是以
是以 为首项,
为首项, 为公比的等比数列.
为公比的等比数列.
 ,
, .
.(2)证法一:由(1)知
 ,
,




 ,
, 原不等式成立.
原不等式成立.证法二:设
 ,
,则

 ,
, 当
当 时,
时, ;当
;当 时,
时, ,
, 当
当 时,
时, 取得最大值
取得最大值 .
. 原不等式成立.
原不等式成立.(3)证明:由(2)知,对任意的
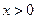 ,有
,有

 .
. 取
取 ,
,则
 .
. 原不等式成立.
原不等式成立.略

练习册系列答案
相关题目
 的前n项和为
的前n项和为 ,且
,且
 ,求证:数列
,求证:数列 是等比数列;
是等比数列;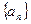 中
中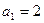 ,点
,点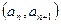 在函数
在函数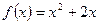 的图象上,
的图象上,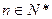 .数列
.数列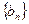 的前n项和为
的前n项和为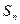 ,且满足
,且满足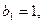 当
当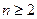 时,
时,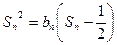
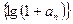 是等比数列;
是等比数列;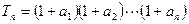 ,
,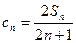 ,求
,求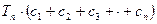 的值.
的值.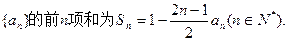
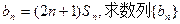 的通项公式;
的通项公式;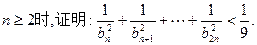
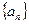 的前
的前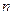 项和为
项和为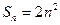 ,
,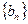 为等比数列,且
为等比数列,且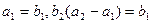 .
.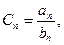 求数列
求数列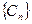 的前n项和
的前n项和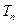 。
。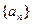 满足
满足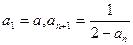 (n≥1)(
(n≥1)(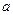 ≠2)
≠2)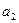 ,
,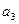 ,
,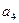 ;
; 中,若
中,若 ,则此数列的前
,则此数列的前 项的和为 .
项的和为 .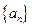 中,
中, 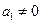 ,
,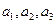 成等差数列;
成等差数列; 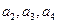 成等比数列;
成等比数列;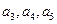 的倒数成等差数列.则①
的倒数成等差数列.则①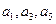 成等差数列;②
成等差数列;② 中,
中, ,且
,且 ,
, .
.