题目内容
若集合A={x|x2-2x-3=0}，B={x|ax-2=0}满足A∩B=B，求实数a组成的集合．
考点：交集及其运算
专题：集合
分析：先解出集合A和B，再根据A∩B=B，得出集合B，然后求解．
解答：
解：A={-1，3}，又A∩B=B，则B⊆A，
∴B=∅，B={-1}，B={3}，
B=∅时，a=0，
B={-1}时，a=-2；
B={3}，a=
，
所以实数a组成的集合是{0，-2，
}．
∴B=∅，B={-1}，B={3}，
B=∅时，a=0，
B={-1}时，a=-2；
B={3}，a=
| 2 |
| 3 |
所以实数a组成的集合是{0，-2，
| 2 |
| 3 |
点评：本题主要考查集合间的运算，注意讨论字母a．
练习册系列答案
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
相关题目
某研究机构对高三学生的记忆力x和判断力y进行统计分析，所得数据如表所示：
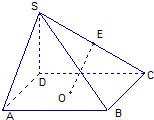已知四棱锥S-ABCD中，底面ABCD为正方形，SD⊥DA，E为SC的中点，O为正方形ABCD的中心，AB=SD=6．
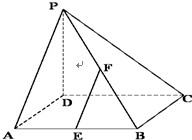如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD=DC，E，F分别是AB，PB的中点．