题目内容
已知函数f(x)=ax-logax(a>0),若使f(x)恒有两个零点,则a的取值范围为 .
考点:函数零点的判定定理
专题:函数的性质及应用
分析:函数y=ax与y=logax关于y=x对称,只需要讨论与y=x有两个解即可,构造函数h(x)=ax-x,只须h(x)的最小值小于0,进而得到实数a的取值范围.
解答:
解:∵函数f(x)=ax-logax(a>0),使f(x)恒有两个零点,
∴f(x)=ax-logax=0,
即ax=logax,
由于函数y=ax与y=logax关于y=x对称,
只需要讨论与y=x有两个解即可,
令h(x)=ax-x,则函数h(x)有两个零点,
当0<a<1时,函数h(x)为减函数,至多有一个零点不满足要求,
当a>1时,令h′(x)=axlna-1=0,则x=loga
,
当0<x<loga
时,h′(x)<0,此时函数h(x)为减函数;
当x>loga
时,h′(x)>0,此时函数h(x)为增函数;
故当x=loga
时,函数h(x)取最小值,
若函数h(x)有两个零点,则h(loga
)<0,
即aloga
<loga
即
=logae<loga
,
即e<
,
即0<lna<
,
即1<a<e
,
故实数a的取值范围是(1,e
),
故答案为:(1,e
)
∴f(x)=ax-logax=0,
即ax=logax,
由于函数y=ax与y=logax关于y=x对称,
只需要讨论与y=x有两个解即可,
令h(x)=ax-x,则函数h(x)有两个零点,
当0<a<1时,函数h(x)为减函数,至多有一个零点不满足要求,
当a>1时,令h′(x)=axlna-1=0,则x=loga
| 1 |
| lna |
当0<x<loga
| 1 |
| lna |
当x>loga
| 1 |
| lna |
故当x=loga
| 1 |
| lna |
若函数h(x)有两个零点,则h(loga
| 1 |
| lna |
即aloga
| 1 |
| lna |
| 1 |
| lna |
即
| 1 |
| lna |
| 1 |
| lna |
即e<
| 1 |
| lna |
即0<lna<
| 1 |
| e |
即1<a<e
| 1 |
| e |
故实数a的取值范围是(1,e
| 1 |
| e |
故答案为:(1,e
| 1 |
| e |
点评:本题考查的知识点是根的存在性及根的个数判断,反函数,导数法判断函数的单调性,导数法求函数的最值,对数的运算性质,是指数函数,对数函数,函数零点,导数等的综合应用,运算量大,综合性可,转化困难,属于难题.

练习册系列答案
相关题目
过双曲线
-
=1的左焦点F作直线l交双曲线于A、B两点,若|AB|=5,则这样的直线共有( )
| x2 |
| 4 |
| y2 |
| 5 |
| A、1条 | B、2条 | C、3条 | D、4条 |
种植某种树苗,成活率为0.9,现采用随机模拟的方法估计该树苗种植5棵恰好4棵成活的概率,先由计算机产生0到9之间取整数值的随机数,指定1至9的数字代表成活,0代表不成活,再以每5个随机数为一组代表5次种植的结果.经随机模拟产生如下30组随机数:
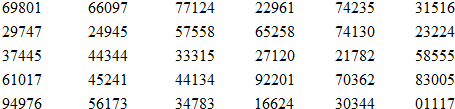
据此估计,该树苗种植5棵恰好4棵成活的概率为( )
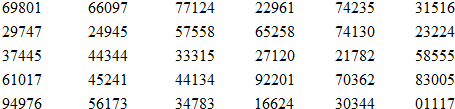
据此估计,该树苗种植5棵恰好4棵成活的概率为( )
| A、0.30 | B、0.35 |
| C、0.40 | D、0.50 |
一物体以速度v(t)=3t2-2t+3做直线运动,它在t=0和t=3这段时间内的位移是( )
| A、9 | B、18 | C、27 | D、36 |
若函数y=f(x)在R上可导,且满足不等式
<-f′(x)lnx恒成立,且常数a,b满足a>b,则下列不等式一定成立的是( )
| f(x) |
| x |
| A、f(b)lna<f(a)lnb |
| B、f(a)lna>f(b)lnb |
| C、f(a)lna<f(b)lnb |
| D、f(b)lna>f(a)lnb |
设集合A={x|
≥0},B=[0,1],那么“m∈A”是“m∈B”的( )
| x |
| 1-x |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要 |