题目内容
19.若存在正整数m,使得f(n)=(2n-7)3n+9(n∈N*)都能被m整除,则m的最大值为6.分析 我们将n=1,2,3,4依次代入,计算相应的f(n)的值,由此不难得到满足条件的m值,然后再根据数学归纳法对结论进行证明.
解答 解:由f(n)=(2n-7)•3n+9,得f(1)=-6,
f(2)=-3×6,f(3)=-3×6,f(4)=15×6,由此猜想m=6.
下面用数学归纳法证明:
(1)当n=1时,显然成立.
(2)假设n=k时,f(k)能被6整除,
即f(k)=(2k-7)•3k+9能被6整除;
当n=k+1时,[2(k+1)-7]•3k+1+9=3[(2k-7)•3k+9]+18(3k-1-1),
由于3k-1-1是2的倍数,故18(3k-1-1)能被6整除.
这就是说,当n=k+1时,f(n)也能被6整除.
由(1)(2)可知对一切正整数n都有f(n)=(2n+7)•3n+9能被6整除,
m的最大值为6,
故答案为:6.
点评 本题考查数学归纳法的应用,考查学生的观察能力,考查推理、论证的能力,运算难点,属于难题.

练习册系列答案
相关题目
7.已知双曲线kx2-2ky2=4的一条准线是y=1,则实数k的值是( )
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | 1 | D. | -1 |
11.sin(-$\frac{13π}{4}$)的值为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | -$\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | -$\frac{{\sqrt{3}}}{2}$ |
8.若f'(x0)=2,则$\lim_{△x→0}\frac{{f({x_0})-f({x_0}+△x)}}{△x}$=( )
| A. | -1 | B. | -2 | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
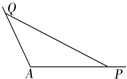 如图,角A为钝角,且sinA=$\frac{3}{5}$,点P、Q分别是在角A的两边上不同于点A的动点.
如图,角A为钝角,且sinA=$\frac{3}{5}$,点P、Q分别是在角A的两边上不同于点A的动点.