题目内容
1.甲、乙两人玩猜数字游戏,先由甲任想一个数字,记为a,再由乙猜甲刚才想的数字,把乙猜的数字记为b,且a,b∈[0,2],若|a-b|≤1,则称“甲乙心有灵犀”,现任意找两个人玩这个游戏,求他们“心有灵犀”的概率.分析 根据条件作出不等式组对应的平面区域,求出对应的面积,结合几何概型的概率公式进行求解即可.
解答 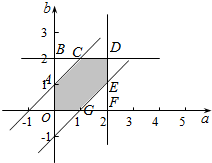 解:∵a,b∈[0,2],
解:∵a,b∈[0,2],
∴$\left\{\begin{array}{l}{0≤a≤2}\\{0≤b≤2}\end{array}\right.$,
则甲乙心有灵犀满足的条件为$\left\{\begin{array}{l}{0≤a≤2}\\{0≤b≤2}\\{|a-b|≤1}\end{array}\right.$,
作出不等式组对应的平面区域如图:
则G(1,0),F(2,0),E(2,1),
则三角形GFE的面积S=$\frac{1}{2}×1×1$=$\frac{1}{2}$,
则正方形OBDF的面积S=2×2=4,
则阴影部分的面积S=4-2×$\frac{1}{2}$=4-1=3,
则他们“心有灵犀”的概率P=$\frac{3}{4}$.
点评 本题主要考查概率的计算,根据几何概型的概率公式,结合线性规划求出对应区域的面积是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知抛物线y2=8x焦点与双曲线$\frac{x^2}{a^2}-{y^2}=1$(a>0)的右焦点重合,则此双曲线的离心率是( )
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $2\sqrt{3}$ |
12.若x∈(1,e),a=ln x,b=(ln x)2,c=ln(ln x),则a,b,c的大小关系为( )
| A. | c>b>a | B. | b>c>a | C. | a>b>c | D. | b>a>c |
16.已知函数f(x)=$\left\{\begin{array}{l}{2x-1,-1<x≤2}\\{{x}^{2}-2,2<x<3}\end{array}\right.$,则不等式f(x)>x的解集为( )
| A. | (1,3) | B. | (-∞,1)∪(3,+∞) | C. | {2} | D. | (1,2)∪(2,3) |